Chat: Neural Networks and Deep Learning

By 苏剑林 | June 06, 2015

Among all machine learning models, perhaps the most interesting and profound is the neural network model. I would like to share my humble opinion and talk about neural networks. Of course, this article does not intend to introduce neural networks from scratch; I am simply discussing my personal understanding of them. For friends who wish to further understand neural networks and deep learning, please refer to the following tutorials:

http://deeplearning.stanford.edu/wiki/index.php/UFLDL Tutorial
http://blog.csdn.net/zouxy09/article/details/8775360

Machine Classification

Using classification as an example: in data mining or machine learning, there are many classification problems. For instance, classifying a sentence as "positive" or "negative," or more finely into categories like happy, angry, or sad. Another typical classification problem is handwritten digit recognition, which involves classifying images into 10 categories (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Consequently, many classification models have been developed.

Classification models are essentially performing fitting—a model is actually a function (or a family of functions) with some undetermined parameters. Based on existing data, a loss function is defined (the most common loss function is the sum of squared errors; readers unfamiliar with this can recall the process of the least squares method). The loss function is then optimized to be as small as possible to find the parameter values. Once the parameters are found, the function can be used for prediction. This is the basic idea of classification; as for preventing overfitting, that is a matter of detail and will not be discussed here for now.

The above idea seems simple, but it presents two fundamental and difficult problems: 1. What are the independent variables of the function? 2. What is this function itself? In other words, how do I know which things (features) are helpful for the classification I want? Secondly, complex non-linear phenomena are ubiquitous; once those features are found, how do I know which function to use to fit them? In fact, there have been no good answers to these two questions for a long time. Prior to the emergence of deep learning, the selection of models and features was basically done manually. In other words, despite decades of development in the field of machine learning, these two fundamental questions remained unresolved!

The emergence of deep learning has brought great hope for solving these two problems. The foundation of deep learning is the neural network.

Neural Networks

Neural networks solve the second problem: what is this function? Traditional models, such as linear regression and logistic regression, basically require us to manually specify the form of the function. However, there are so many non-linear functions that simply providing a few existing functions often yields limited fitting results. Furthermore, the effectiveness of fitting depends heavily on finding good features—which brings us back to the first unresolved problem: what are the independent variables? (For example, if a function is $y=x^2+x$, a quadratic non-linear function, fitting it with linear regression will never yield good results. However, if I define a new feature $t=x^2$, then $y=t+x$ is a linear function with respect to $t$ and $x$, which can be solved by a linear model. The problem is, without knowing the specific form of $y$, how do we find the feature $t=x^2$? This basically relies on experience and luck.)

To solve the problem of "what is this function," there are several ideas. For instance, we have learned Taylor series and know that general non-linear functions can be approximated through Taylor expansions. Thus, a natural thought is: why not use high-degree polynomials to approximate them? Polynomial fitting is indeed a good idea, but anyone who has studied computational methods probably knows that the problem with polynomial fitting is that it fits very well within the training data but performs poorly on test data—a phenomenon known as overfitting. So, is there another way? Yes! The founders of neural networks suggested—use composite functions to fit!

That's right, neural networks fit through multiple composite functions! And it is the simplest type of function composition—one being a linear function and the other being the simplest non-linear function: the binary function $\theta(x)$:

Taking a simple three-layer neural network for a binary classification problem as an example:

First, the input features are combined linearly with weights (weights $w^{(1)}_{j,i}$), and then in the hidden layer, a $\theta(x)$ transformation is applied to the combined result. Then, those results are combined linearly again (weights $w^{(2)}_{k,j}$) and processed by another $\theta(x)$ at the output layer for the final output. The entire process consists of two linear combinations and two $\theta(x)$ operations, alternating between them. Thus, the whole process is a double composite function:

The non-linear function $\theta(x)$ is called the activation function. Next, we need to define a loss function, which is the function to be optimized to its minimum. However, the optimization process involves derivatives, and $\theta(x)$ is discrete and cannot be differentiated. Therefore, continuous activation functions are usually used to replace it, such as the Sigmoid function:

The question now is whether the proposed model truly possesses the formidable power we imagine. The following quote highlights the power of neural networks:

In 1943, psychologist W.S. McCulloch and mathematical logician W. Pitts established the neural network described above and its corresponding mathematical model, known as the MP model. Through the MP model, they proposed a formalized mathematical description and structural method for neurons, proving that a single neuron could perform logical functions. Note that being able to perform logical functions means it can perform everything that computers today can do—modern computers are simply combinations of a series of logical instructions. (Of course, there is the matter of speed; without considering speed, the MP model can indeed perform all tasks that current computers can perform.)

Deep Learning

The above mentions only double composite functions. Readers can easily imagine that since this path is feasible, then using triple, quadruple, or even more layers of composite functions should yield better results. Exactly, this is the original idea of deep learning. After talking so much, we have finally arrived at deep learning.

Neural networks, including multi-layered neural networks, are not models that were just published recently. In fact, people published these models and proposed some solution algorithms decades ago. So, what exactly is the difference between deep learning and previous neural networks? Common answers include: deep learning usually involves many layers (having five or six hidden layers is common), and it introduces more effective solution algorithms that can better handle problems like gradient explosion or converging to local minima. But I believe these are not the essential differences. I think the difference between deep learning and traditional neural networks lies in the fact that deep learning is dedicated to solving the first problem we mentioned: What are the independent variables of the function?

In other words, deep learning algorithms are used to discover good features, a task that was previously performed manually and where the results were not necessarily "good." Now, machines can automatically (unsupervisedly) complete this task, and the results are no worse than those selected by humans. Once good features are found, even linear models can perform quite well. Therefore, it is said that deep learning has pushed the field of artificial intelligence a large step forward and is called the algorithm closest to artificial intelligence at present.

Why dedicate efforts to selecting good features? This is for several reasons:

First, accuracy: Finding good features means better exclusion of interference factors, ensuring that the model inputs are beneficial and reducing redundancy;

Second, computational volume: For example, for image classification, if an image is $1000 \times 1000$ pixels, inputting all pixels directly means $10^6$ features. If all these features are fed into a deep learning model, the number of parameters could reach $10^{12}$ or even more. Solving such a model is nearly impossible. Finding good features means inputting only useful information into the model, thereby reducing the number of parameters and making calculation possible;

Third, storage volume: Good feature algorithms can often also be used for effective file compression, reducing storage requirements and the memory needed during training.

Autoencoder

How does deep learning achieve the above functionality? Two words: Information Loss!

First, we need to realize that no matter how intelligent our algorithms are, they are designed to complete a certain task in a certain field. Therefore, it is certain that the original data contains information we don't need, and it's even possible that unnecessary information is more abundant than necessary information. If there were a way to remove this unnecessary information so that only the useful information remains, how great would that be! (Information loss, in an ideal case, loses the information we don't need). Perhaps everyone hasn't realized yet that our human brain does the same thing all the time. We call that thinking process—Abstraction!

Yes, abstraction. Abstraction is a process of information loss. For example, there's a pile of balls: basketballs, soccer balls, volleyballs, ping-pong balls, etc. Our first thought is: they are all (approximately) "spheres"—a set of points equidistant from a certain center! But don't forget, this is a pile of distinct balls; their sizes, colors, and materials are all different. By identifying them as "balls," we discard information about size, color, and material, leaving only the common feature—a roughly spherical shape. Such a process is exactly our abstract thinking, and it is also a process of information loss!

How does deep learning achieve this process? The "Autoencoder" is one of its core components, and it is also based on neural networks. Please look at the following three-layer neural network:

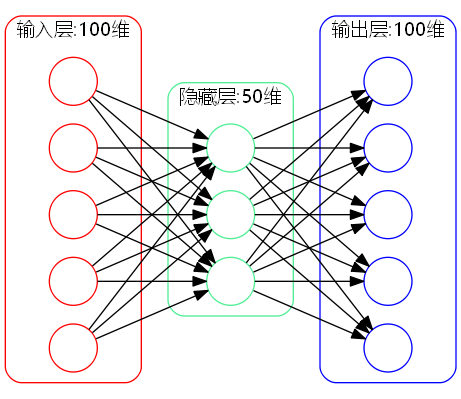
The input and output of the network are the same (both are 100-dimensional), while the hidden nodes in the middle are 50-dimensional. The autoencoder hopes to train a simple identity function $x=x$ through this neural network, meaning it hopes the input and output are the same. However, during the training process, the dimensionality decreases from 100 to 50 from the input layer to the hidden layer, which means information is lost. Yet, from the hidden layer to the output layer, the dimensionality returns to 100. Since information has already been lost, theoretically, this reconstruction process should be impossible.

However, we insist on forcing it to train this way. What result will we get? The machine has no choice but to reconstruct the original data from these 50-dimensional values as best as it can. To make the reconstruction as good as possible, the machine must extract the common features of a large batch of input data as the reconstruction result. As a simple example, please look at the following four images:

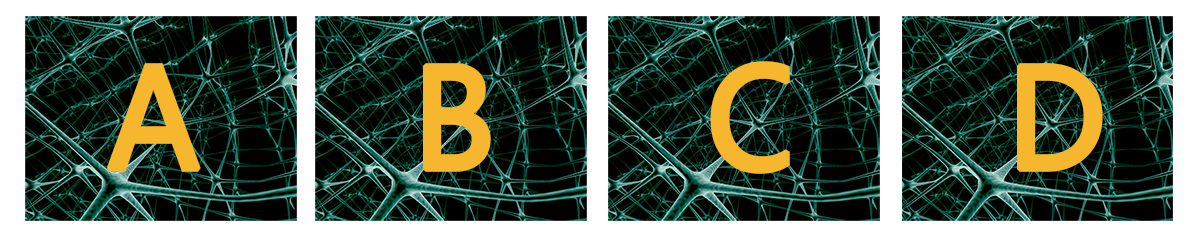
These are four different images. How do readers perceive the differences between them? Obviously, the background of the images is the same; the difference lies in the letters on the images. If I asked you to remember the differences between these images in a short time, you would only be able to remember the letters on the images. But don't forget these are four complete images; by remembering only the four letters, we have ignored the backgrounds entirely—losing most of the information!

But if our task is just to "recognize the letters on the image," then ignoring the background is completely correct! After removing the background, we have the "good features" for making judgments. The presence of the background would actually be an interference.

This is the process of autoencoding, the process of information loss, and the process of abstraction!

Summary

Of course, deep learning is very rich in content and has various variations. It is worth mentioning that many models based on deep learning have achieved State of the Art effects (the most advanced), showing the power of deep learning.

This article is not an introductory tutorial on deep learning; it is merely my shallow understanding of neural networks and deep learning. If readers want to systematically study the relevant theories, it is best to first read some books on data mining and machine learning to understand the basic concepts, and then read the two articles mentioned at the beginning.

http://ufldl.stanford.edu/wiki/UFLDL Tutorial
http://blog.csdn.net/zouxy09/article/details/8775360