A Brief Exploration of OCR Technology: 3. Feature Extraction (2)

By 苏剑林 | June 18, 2016

Layer-by-layer Recognition

Once the image is effectively layered, we can further design corresponding models based on our previous assumptions to identify text regions in the image through layer-by-layer processing.

Connectivity

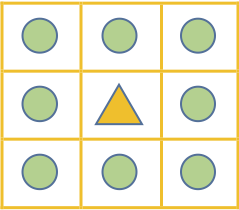
8-connectivity

As can be seen, each layer of the image consists of several connected components. Since text itself is composed of relatively dense strokes, it often forms a connected region. The "connected" property here is defined as 8-connectivity, meaning the 8 pixels surrounding a specific pixel are defined as adjacent pixels, and adjacent pixels are defined as belonging to the same connected region.

After defining connected regions, each layer is segmented into several connected components. In other words, we gradually decompose the original image, as shown in Figure 9.

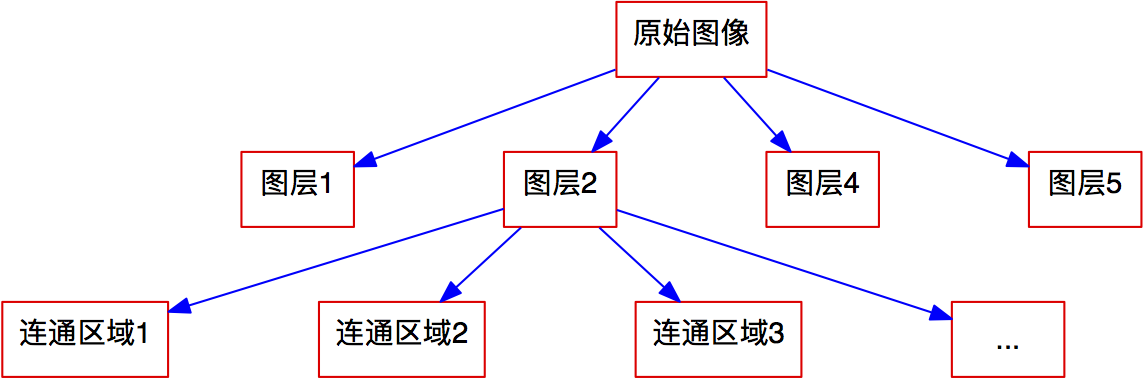
Figure 9: Image Decomposition Structure Diagram

Erosion Resistance

Once the image is decomposed to the level of connected regions, we stop further subdivision and start identifying which regions are potential text areas. Here we require the text to have a certain degree of erosion resistance. Therefore, we first define erosion.

Erosion is a morphological transformation on images, generally targetted at binary images. For non-zero pixels (pixels with a value of 1) in a binary image, if all its adjacent pixels are 1, it remains unchanged; otherwise, it becomes 0. Here we also use the 8-connectivity definition. It can be observed that if the boundary of a connected region is longer, the "damage" caused by the erosion operation is greater; conversely, if the boundary is shorter, the "damage" is smaller.

Based on the definition of erosion above, we can state a requirement for text regions:

Erosion Resistance Requirement: The connected region where the text is located should possess a certain degree of erosion resistance.

Here, "certain degree" refers to a continuous range—it cannot be too large or too small. For example, a square region with a large area has very strong erosion resistance because its boundary line is very short, but such regions are clearly not text regions; the rice cooker in Layer 5 of the previous article's decomposition belongs to this type. Additionally, erosion resistance cannot be too weak; for instance, thin lines might disappear after erosion. These are not considered candidate text regions either; the text boundaries in Layer 4 of the previous article's decomposition belong to this type.

We can define an indicator for erosion resistance:

After testing, the erosion resistance of text regions is roughly in the range of $[0.1, 0.9]$.

After filtering the 5 decomposed layers based on erosion resistance, we obtain the following feature layers.

Feature Layer 1

Feature Layer 2

Feature Layer 3

Feature Layer 4

Retain only connected regions with erosion resistance in the $[0.1, 0.9]$ range

Pooling Operation

Up to this point, we have obtained 5 feature layers. Although it is visible to the naked eye that the text is mainly concentrated in the 5th feature layer, for general images, text may be distributed across multiple feature layers. Therefore, feature integration is required. Our method for integrating features here is similar to "pooling" in convolutional neural networks, which is why we borrowed the name.

First, we superimpose the 5 feature layers to obtain an overall image feature (called the superimposed feature). Such a feature can be used as the final output, but it is not the best approach. We believe that the main text features within a certain area should already be concentrated in a specific feature layer rather than scattered across all layers. Therefore, after obtaining the superimposed feature, we use a method similar to "Max Pooling" to integrate the features, as follows:

1. Directly superimpose the features, then determine the connected regions of the superimposed features;
2. Detect which feature layer contributes the most to each connected region; the region then only retains the source from that specific feature layer.

After this pooling operation, the final feature result is shown in Figure 11.

Figure 11: Features After Pooling

Post-processing

For the image we are demonstrating, the feature map in Figure 11 obtained after the above operations requires no further processing. However, for general images, some poorly handled regions may remain, which need to be further excluded. The exclusion process mainly consists of two steps: Low/High-density area exclusion and Isolated area exclusion.

Density Exclusion

One type of connected region that is clearly not text is a low-density region. A typical example is a connected region formed by table lines; such a region has a large extent but contains very few pixels, meaning it has low density. Such regions can be excluded. First, we define connected region density and low-density regions:

Connected Region Density: Starting from a connected region, we can find its horizontal bounding box. The density of this region is defined as: \begin{equation} \text{Connected Region Density} = \frac{\text{Area of Connected Region}}{\text{Area of Bounding Box}} \times \frac{\text{Total Area of Original Image}}{\text{Area of Bounding Box}} \tag{8} \end{equation}

Low-Density Region: If the density of a connected region is less than 16, then this connected region is defined as a low-density region.

Intuitively, the definition should be $\frac{\text{Area of Connected Region}}{\text{Area of Bounding Box}}$, but an extra factor $\frac{\text{Total Area of Original Image}}{\text{Area of Bounding Box}}$ is included here to incorporate the influence of the region's size. Because text typically has clear boundaries and is easily segmented, generally, the larger the area a region occupies, the less likely it is to be a text region. The parameter 16 is an empirical value.

Low-density exclusion is an effective method for removing non-text areas with many lines, such as tables. Similarly, large High-density areas are also a category of regions that need exclusion. Once low-density regions are defined, it becomes easy to define high-density regions:

High-Density Region Definition (v1): If the region formed by inverting a connected region within its horizontal bounding box is a low-density region, then the connected region is defined as a high-density region.

While this definition is natural, it has some irrationalities. For example, the character "一" (one) is a horizontal rectangle, so the density after inversion is 0, leading to the character "一" being excluded, which is incorrect. A solution to this problem is:

High-Density Region Definition: A region is defined as a high-density region if and only if the following condition is met: \begin{equation} \frac{1 + \text{Area of Bounding Box} - \text{Area of Connected Region}}{\text{Area of Bounding Box}} \times \frac{\text{Total Area of Original Image}}{\text{Area of Bounding Box}} < 16 \tag{9} \end{equation}

This adds 1 to the original definition, preventing the case where the density becomes 0 after inversion.

There is another case where this fails: if the input image is a single character. In this case, there is only one connected region, and $\frac{\text{Total Area of Original Image}}{\text{Area of Bounding Box}}$ is close to 1, thus it might be judged as a low-density region and wrongly excluded. This situation is indeed difficult to balance. A feasible solution is to manually specify whether the mode is single character, single line, or full image; Google's Tesseract OCR also provides such options.

Isolated Region Exclusion

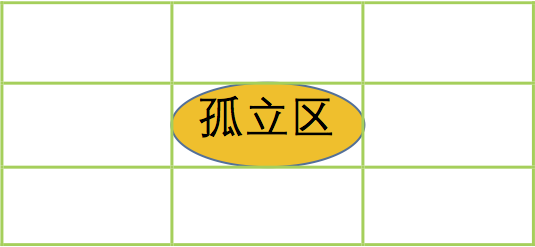
Figure: Isolated Region Demo

The premise of isolated region exclusion is that text characters and strokes should be relatively compact. If a region is clearly isolated from other regions, it is likely not a text region. In other words, isolated regions can be excluded. First, we define the concept of an isolated region:

Isolated Region: Starting from a connected region, find its horizontal bounding box. Expand this rectangle center-symmetrically so that its area becomes 9 times the original (length and width become 3 times the original, as shown in the left figure). If the expanded region does not contain any other connected regions, then the original connected region is called an isolated region.

In most cases, isolated region exclusion is a very simple and effective denoising method because many noise points are isolated. However, isolated region exclusion carries certain risks. If an image contains only one character, forming a single connected region, then this region will be isolated and thus excluded. Therefore, additional constraints should be added to isolated region exclusion. One optional extra constraint is that the ratio $\frac{\text{Area of Connected Region}}{\text{Area of Bounding Box}}$ for the excluded isolated region must be greater than 0.75 (this value originates from the area ratio of a circle to its circumscribed square, $\pi/4$).