Preliminary Exploration of OCR Technology: 7. Language Models

By 苏剑林 | June 26, 2016

Due to reasons such as image quality, even the best-performing recognition models can have the possibility of recognition errors. To reduce the recognition error rate, the recognition problem can be combined with statistical language models, and the optimal recognition result can be provided through dynamic programming methods. This is one of the important methods for improving OCR recognition performance.

Transition Probability

In the process of analyzing our experimental results, we encountered the following case. Due to possible reasons such as image blurriness, the word "电视" (television) was recognized as "电柳" (electric willow). Using the image model alone cannot resolve this problem effectively because, from the image model's perspective, "电柳" appeared to be the optimal choice. However, a language model can solve this problem quite ingeniously. The reason is simple: based on a large amount of text data, we can calculate the probabilities of the word "电视" and the word "电柳." We find that the probability of "电视" is far greater than that of "电柳," so we would believe the word is "电视" rather than "电柳."

From a probabilistic perspective, for the recognition result $s_1$ of the first character region, our previously mentioned convolutional neural network provides two candidate characters: "电" and "宙" (selecting only the top two, as the probabilities of others are too small). The probabilities $W(s_1)$ for each candidate character are $0.99996$ and $0.00004$, respectively. For the recognition result $s_2$ of the second character region, the CNN provides "柳" (willow), "视" (vision), and "规" (rule) (selecting only the top three). The probabilities $W(s_2)$ for each candidate character are $0.87838$, $0.12148$, and $0.00012$, respectively. Therefore, there are effectively six combinations: "电柳", "电视", "电规", "宙柳", "宙视", "宙规".

Now consider their transition probabilities. The so-called transition probability is actually the conditional probability $P(s_2|s_1)$, which is the probability of $s_2$ appearing given that $s_1$ has occurred. By statistics from 100,000 WeChat texts, we found that the character "电" appeared $145,001$ times, while the sequences "电柳", "电视", and "电规" appeared $0$, $12,426$, and $7$ times, respectively. The character "宙" appeared $1,980$ times, while "宙柳", "宙视", and "宙规" appeared $0$, $0$, and $18$ times. Thus, we can calculate:

The results are shown in the figure below:

Figure 20 Considering Transition Probabilities

From a statistical perspective, the optimal combination of $s_1, s_2$ should maximize the following expression (14):

Therefore, we can calculate that the best combination of $s_1, s_2$ is "电视" rather than "电柳". In this way, we have successfully obtained the correct result through statistical methods, thereby improving the accuracy rate.

Dynamic Programming

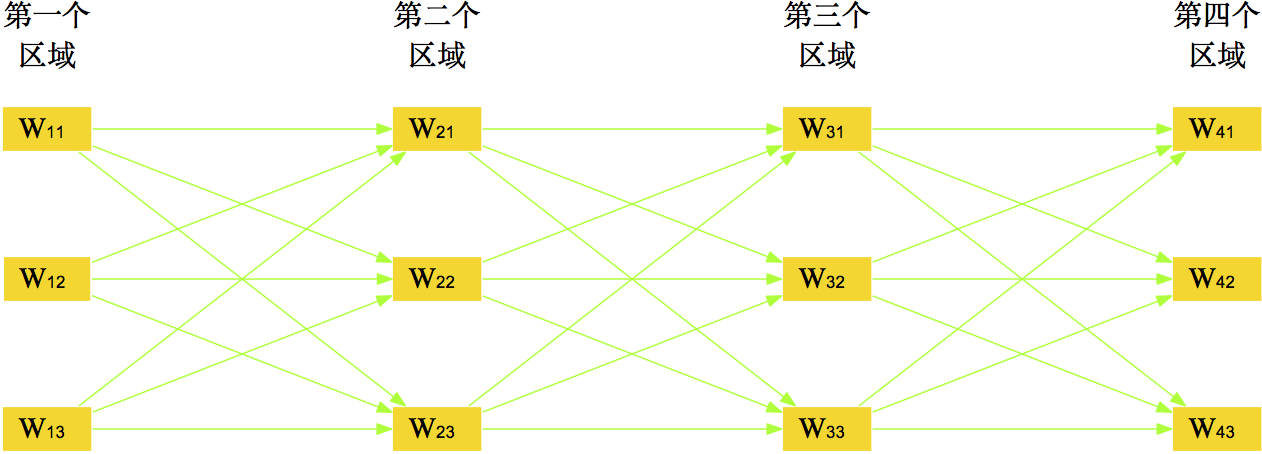
Figure 21 Programming problem for multi-character images

Similarly, as shown in Figure 21, if a single-line text image has $n$ characters $s_1, s_2, \dots, s_n$ to be determined, then we should maximize:

This is the core idea of statistical language models. Many fields of natural language processing, such as Chinese word segmentation, speech recognition, and image recognition, use the same method [6]. There are two main problems to solve here: (1) Estimation of each $P(s_{i+1}|s_i)$; (2) How to solve for the maximum value of $f$ given each $P(s_{i+1}|s_i)$.

Transition Probability Matrix

For the first problem, it is only necessary to count the number of occurrences of $s_i$, denoted as $\#s_i$, and the number of times $s_i, s_{i+1}$ appear contiguously, denoted as $\#(s_i, s_{i+1})$, from a large corpus, and then let

This is inherently not difficult. There are 3062 recognition targets in this paper, so theoretically, it should generate a $3062 \times 3062$ matrix, which is very large. Of course, this matrix is very sparse, and we only need to save the valuable elements.

Now, we must focus on the case where $\#(s_i, s_{i+1}) = 0$. In the previous section, we simply took $P(s_{i+1}|s_i) = 0$, but in Fact, this is unreasonable. Just because something does not appear doesn't mean it cannot appear; it just means the probability is very small. Therefore, even for $\#(s_i, s_{i+1}) = 0$, a small probability should be assigned instead of 0. This is known in statistics as the data smoothing problem.

A simple smoothing method is to add a small positive constant $\alpha$ (e.g., 1) to the frequencies of all terms (including terms with a frequency of 0), then recalculate the total and the frequency, so that every item receives a positive probability. This approach may lower the probability of high-frequency terms, but since the probabilities here only have relative significance, this impact is not obvious (a more reasonable approach is to add the constant only when the frequency is below a certain threshold $T$). Using this approach, from hundreds of thousands of WeChat articles, we calculated a transition probability matrix with 1.6 million adjacent Chinese character pairs.

Viterbi Algorithm

For the second problem, solving for the optimal combination $s_1, s_2, \dots, s_n$ belongs to the problem of finding the optimal path in dynamic programming, for which the most effective method is the Viterbi algorithm [6].

The Viterbi algorithm is a simple and efficient algorithm that can be implemented in Python with about a dozen lines of code. Its core idea is: if the final optimal path passes through a certain $s_{i-1}$, then the path from the starting node to $s_{i-1}$ must also be an optimal path—because each node $s_i$ only affects the preceding and following probabilities $P(s_i|s_{i-1})$ and $P(s_{i+1}|s_i)$.

Based on this idea, a recursive method can be used. When considering each $s_i$, one only needs to find the optimal path among all candidates passing through each $s_{i-1}$ and then combine it with the current $s_i$ for comparison. In this way, each step only requires no more than $l^2$ calculations to step-by-step find the optimal path. The efficiency of the Viterbi algorithm is $O(n \cdot l^2)$, where $l$ is the maximum number of candidates for node $s_i$. It is proportional to $n$, making it very efficient.

Enhancement Effect

Experiments show that combining statistical language models with dynamic programming can effectively resolve cases of misrecognition between visually similar characters. In our tests, it corrected several errors as follows:

电柳 (Electric Willow) → 电视 (Television)
研友 (Research Friend) → 研发 (R&D)
速于 (Fast in) → 速干 (Quick dry)
围像 (Surrounding image) → 图像 (Image)
...

Dynamic programming via statistical language models can correct many recognition errors.

Since the corpus used to generate the transition matrix is not large enough, there is still significant room for improvement in correction results. Nonetheless, due to the simplicity and efficiency of the Viterbi algorithm, this is a highly cost-effective step.