A Brief Reading of "Attention is All You Need" (Introduction + Code)

By 苏剑林 | January 06, 2018

In mid-2017, there were two similar papers that I particularly appreciated: Facebook's "Convolutional Sequence to Sequence Learning" and Google's "Attention is All You Need". Both are innovations in Seq2Seq, and essentially, both abandon the RNN structure to perform Seq2Seq tasks.

In this blog post, I will provide a simple analysis of "Attention is All You Need". Since both papers are quite popular and there are already many interpretations online (though many are direct translations of the paper with little personal insight), I will try to use my own words as much as possible and avoid repeating what others have already said.

Sequence Encoding

The standard approach for Deep Learning in NLP is to first tokenize a sentence and then convert each word into a corresponding word vector sequence. Thus, each sentence corresponds to a matrix $\boldsymbol{X}=(\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_t)$, where $\boldsymbol{x}_i$ represents the word vector (row vector) of the $i$-th word with dimension $d$. Therefore, $\boldsymbol{X}\in \mathbb{R}^{n\times d}$. The problem then becomes how to encode these sequences.

The first basic idea is the RNN layer. The RNN approach is simple and recursive:

Whether it is the widely used LSTM, GRU, or the more recent SRU, none have departed from this recursive framework. RNN structures are simple and well-suited for sequence modeling, but a glaring drawback is their lack of parallelization, resulting in slower speeds—a natural defect of recursion. Additionally, I personally feel that RNNs cannot easily learn global structural information because they are essentially Markov decision processes.

The second idea is the CNN layer. The CNN approach is also quite natural, using a window-based traversal. For example, a convolution with a window size of 3 is:

In Facebook's paper, pure convolution was used to achieve Seq2Seq learning. This is an exquisite and extreme case of convolutional use; readers who favor CNNs should definitely read that paper. CNNs are easy to parallelize and can capture some global structural information. I personally prefer CNNs and have tried to replace existing RNN models with CNNs in my current work or competitions, developing my own set of experiences, which we will discuss later.

Google's work provides a third path: Pure Attention! Attention is all you need! While an RNN requires a step-by-step recursion to obtain global information (usually requiring a Bi-RNN), and a CNN captures only local information (requiring stacking layers to increase the receptive field), the Attention approach is blunt: it obtains global information in a single step! Its solution is:

where $\boldsymbol{A},\boldsymbol{B}$ are another sequence (matrix). If we set $\boldsymbol{A}=\boldsymbol{B}=\boldsymbol{X}$, it is called Self Attention. This means directly comparing $\boldsymbol{x}_t$ with every word in the original sequence to calculate $\boldsymbol{y}_t$!

Attention Layer

Definition of Attention

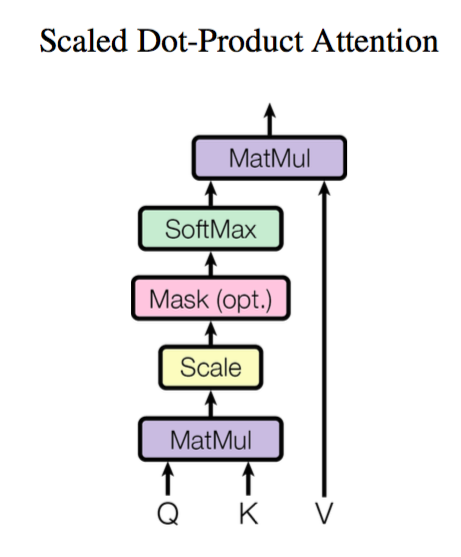
Google's generalized Attention idea is a sequence encoding scheme. Therefore, we can consider it a sequence encoding layer, much like RNNs and CNNs.

While the previous description was a generalized framework, Google's actual implementation is very specific. First, they provide the definition of Attention:

Using the notation from Google's paper, where $\boldsymbol{Q}\in\mathbb{R}^{n\times d_k}, \boldsymbol{K}\in\mathbb{R}^{m\times d_k}, \boldsymbol{V}\in\mathbb{R}^{m\times d_v}$. If we ignore the $softmax$ activation function, it is essentially the multiplication of three matrices of sizes $n\times d_k, d_k\times m, m\times d_v$, resulting in an $n\times d_v$ matrix. We can view this as an Attention layer that encodes an $n\times d_k$ sequence $\boldsymbol{Q}$ into a new $n\times d_v$ sequence.

How do we understand this structure? Let's look at it vector by vector:

where $Z$ is the normalization factor. In fact, $q, k, v$ are short for $query, key, value$. $\boldsymbol{K}$ and $\boldsymbol{V}$ are in a one-to-one correspondence, acting like a key-value pair. The formula means that by using $\boldsymbol{q}_t$ as a query and calculating its dot product with each $\boldsymbol{k}_s$ followed by a softmax, we find the similarity between $\boldsymbol{q}_t$ and each $\boldsymbol{v}_s$, then perform a weighted sum to get a $d_v$-dimensional vector. The factor $\sqrt{d_k}$ acts as a regulator to ensure the dot product doesn't grow too large (which would make the softmax output either 0 or 1, losing its "softness").

In fact, this definition of Attention is not new. However, due to Google's influence, we can say it has been formally proposed as a standalone layer. Furthermore, this definition is just one form of attention; there are other choices, such as using concatenation followed by a dot product with a parameter vector instead of a simple dot product for the query and key, or even not normalizing the weights.

Multi-Head Attention

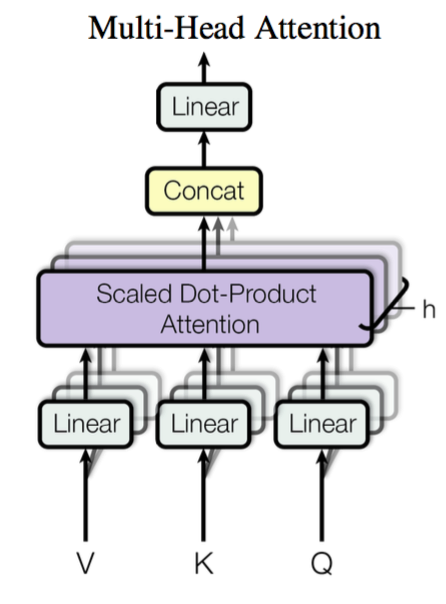
This is a new concept proposed by Google to refine the Attention mechanism. Formally, it is quite simple: $\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V}$ are mapped through parameter matrices, and then Attention is performed. This process is repeated $h$ times, and the results are concatenated. It is truly "simplicity is the ultimate sophistication." Specifically:

Here $\boldsymbol{W}_i^Q\in\mathbb{R}^{d_k\times \tilde{d}_k}, \boldsymbol{W}_i^K\in\mathbb{R}^{d_k\times \tilde{d}_k}, \boldsymbol{W}_i^V\in\mathbb{R}^{d_v\times \tilde{d}_v}$, and then:

The final result is a sequence of $n\times (h\tilde{d}_v)$. The so-called "Multi-Head" simply means doing the same thing several times (with non-shared parameters) and concatenating the results.

Self Attention

So far, the description of the Attention layer has been generalized. We can now look at specific applications. For example, in Reading Comprehension, $\boldsymbol{Q}$ could be the vector sequence of the passage, and by setting $\boldsymbol{K}=\boldsymbol{V}$ as the vector sequence of the question, the output becomes the Aligned Question Embedding.

In Google's paper, most of the Attention used is Self Attention, which is internal attention.

Self Attention is simply $Attention(\boldsymbol{X},\boldsymbol{X},\boldsymbol{X})$, where $\boldsymbol{X}$ is the input sequence. In other words, Attention is performed within the sequence to find internal internal relationships. One of the main contributions of Google's paper is demonstrating that internal attention is extremely important for sequence encoding in machine translation (and general Seq2Seq tasks), whereas previous Seq2Seq research mostly used attention at the decoding end. Similarly, R-Net, a top model on the SQuAD leaderboard, also incorporated a self-attention mechanism, which led to improvements.

More accurately, Google uses **Self Multi-Head Attention**:

Position Embedding

However, if you think about it for a moment, you'll realize that such a model cannot capture the order of the sequence! In other words, if you shuffle the rows of $\boldsymbol{K}$ and $\boldsymbol{V}$ (equivalent to shuffling the word order in a sentence), the Attention result remains the same. This indicates that, so far, the Attention model is essentially just a very sophisticated "bag-of-words" model.

This is a serious problem. As we know, order is crucial information for time series, especially in NLP tasks. It represents local and even global structures. Failing to learn order information significantly degrades performance (for example, in machine translation, every word might be translated correctly, but they won't be organized into a coherent sentence).

So, Google introduced Position Embedding. Each position is assigned an ID, and each ID corresponds to a vector. By combining position vectors with word vectors, each word is imbued with position information, allowing Attention to distinguish words at different positions.

Position Embedding isn't a new concept; it was also used in Facebook's "Convolutional Sequence to Sequence Learning." However, in Google's work, it has a few distinct characteristics:

1. Previously, in RNN or CNN models, Position Embedding was a "nice-to-have" auxiliary tool—it helped, but the models could still capture position information without it (since RNNs and CNNs inherently handle order). But in this pure Attention model, Position Embedding is the only source of position information, making it a core component, not just an auxiliary one.

2. In previous methods, Position Embeddings were usually learned from the tasks. Google, however, provides a formula to construct Position Embeddings: \begin{equation}\left\{\begin{aligned}&PE_{2i}(p)=\sin\Big(p/10000^{2i/{d_{pos}}}\Big)\\ &PE_{2i+1}(p)=\cos\Big(p/10000^{2i/{d_{pos}}}\Big) \end{aligned}\right.\end{equation} This maps position ID $p$ to a $d_{pos}$-dimensional vector where the $i$-th element is $PE_i(p)$. Google noted that they compared learned position vectors with those calculated by the formula, and the results were similar. Therefore, we prefer the constructed ones, which we call Sinusoidal Position Embeddings.

3. Position Embedding represents absolute position, but relative position is also important in language. Google's choice of formula is motivated by the identities $\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$ and $\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$. This means the vector for position $p+k$ can be expressed as a linear transformation of the vector at position $p$, providing the potential to represent relative position information.

There are several ways to combine position and word vectors: concatenating them or making them the same size and adding them. Both Facebook and Google chose addition. Intuitively, adding might lose information, but Google's results show it is an excellent approach. My understanding of this might not be deep enough yet.

Furthermore, although the paper presents the Position Embedding in an interleaved $\sin, \cos$ format, the interleaving itself has no special significance. You could rearrange it arbitrarily (like all $\sin$ then all $\cos$), because:

1. If you concatenate the Position Embedding to the word vector, whether $\sin$ and $\cos$ are interleaved or concatenated makes no difference, as the next step is just a weight matrix transformation.

2. If you add the embedding, there might seem to be a difference. However, word vectors themselves have no inherent local dimension structure. If you shuffle the 50 dimensions of a word vector (consistently across all vectors), it's still equivalent to the original. Since the word vectors have no local structure, there's no need to emphasize the local structure (the interleaving) of the Position Embedding.

A Few Shortcomings

At this point, the Attention mechanism has been basicially introduced. The advantage of the Attention layer is its ability to capture global dependencies in one step because it directly compares sequence elements pairwise (at the cost of $O(n^2)$ computation, though since it's pure matrix operations, this isn't too severe). In contrast, RNNs require step-by-step recursion, and CNNs require stacking layers to expand the receptive field. This is a clear advantage for Attention.

The rest of Google's paper explains how it's used in machine translation, which is more about application and hyperparameter tuning. While Google showed that pure attention achieves state-of-the-art results in MT, I'd like to discuss some shortcomings of the paper and the Attention layer itself.

1. The title is "Attention is All You Need," so the paper intentionally avoids the terms RNN and CNN. However, I feel this is a bit forced. They named a component "Position-wise Feed-Forward Networks," which is essentially a 1D convolution with a kernel size of 1. It feels like they invented a new name just to avoid saying "convolution."

2. While Attention has no direct link to CNNs, it heavily borrows CNN ideas. Multi-Head Attention is doing attention multiple times and concatenating, which matches the idea of multiple kernels in CNNs. They also use residual structures, which originated in CNNs.

3. It cannot model position information well. This is a fundamental weakness. While Position Embedding is a relief, it doesn't fundamentally solve the problem. For example, using pure Attention for text classification or MT might work well, but it might not perform as well for sequence labeling (word segmentation, NER, etc.). Why does it work for MT? Likely because MT doesn't strictly demand word order in the same way, and the evaluation metric BLEU doesn't strictly emphasize order either.

4. Not all problems require long-range global dependencies. Many problems rely on local structures, where pure Attention might not be optimal. In fact, Google seems aware of this and mentions a "restricted" version of Self-Attention where a word only looks at $r$ words before and after it. This makes the complexity $O(nr)$ and captures local structure. But clearly, that's just the concept of a convolution window!

Through this discussion, we can see that treating Attention as a standalone layer and mixing it with CNN or RNN structures should allow for a better fusion of their respective strengths, rather than the "Attention is All You Need" claim, which feels like a bit of an "over-correction." Regarding the paper's work, perhaps a more modest title like "Attention is All Seq2Seq Need" would have been more accurate.

Code Implementation

Finally, to make this post practical, I've provided implementation code for the Multi-Head Attention described in the paper. Readers can use it directly or refer to it for modifications.

Note that while Multi-Head means "repeat it a few times and concatenate," the code shouldn't follow that logic literally, as it would be very slow. TensorFlow does not automatically parallelize independent operations like:

a = tf.zeros((10, 10))
b = a + 1
c = a + 2

The calculations of b and c are serial despite not depending on each other. Therefore, we must merge Multi-Head operations into a single tensor calculation, as the internal logic of a single tensor multiplication is automatically parallelized.

Additionally, we need to apply a Mask to the sequences to ignore padded parts. General masking zeros out the padded portions, but in Attention, the Mask should occur before the softmax by subtracting a large integer from the padded portions (so they become effectively zero after softmax). These are implemented in the code.

TensorFlow Version

Implementation in TF: https://github.com/bojone/attention/blob/master/attention_tf.py

Keras Version

Keras remains one of my favorite frameworks, so I've written one for it too: https://github.com/bojone/attention/blob/master/attention_keras.py

Code Test

A simple test on IMDB using Keras (without Mask):

from __future__ import print_function
from keras.preprocessing import sequence
from keras.datasets import imdb
from attention_keras import *

max_features = 20000
maxlen = 80
batch_size = 32

print('Loading data...')
(x_train, y_train), (x_test, y_test) = imdb.load_data(num_words=max_features)
print(len(x_train), 'train sequences')
print(len(x_test), 'test sequences')

print('Pad sequences (samples x time)')
x_train = sequence.pad_sequences(x_train, maxlen=maxlen)
x_test = sequence.pad_sequences(x_test, maxlen=maxlen)
print('x_train shape:', x_train.shape)
print('x_test shape:', x_test.shape)

from keras.models import Model
from keras.layers import *

S_inputs = Input(shape=(None,), dtype='int32')
embeddings = Embedding(max_features, 128)(S_inputs)
# embeddings = SinCosPositionEmbedding(128)(embeddings) # Adding Position_Embedding can slightly improve accuracy
O_seq = Attention(8,16)([embeddings,embeddings,embeddings])
O_seq = GlobalAveragePooling1D()(O_seq)
O_seq = Dropout(0.5)(O_seq)
outputs = Dense(1, activation='sigmoid')(O_seq)

model = Model(inputs=S_inputs, outputs=outputs)
model.compile(loss='binary_crossentropy',
              optimizer='adam',
              metrics=['accuracy'])

print('Train...')
model.fit(x_train, y_train,
          batch_size=batch_size,
          epochs=5,
          validation_data=(x_test, y_test))

Result without Position Embedding:

Train on 25000 samples, validate on 25000 samples
25000/25000 [==============================] - 9s - loss: 0.4090 - acc: 0.8126 - val_loss: 0.3541 - val_acc: 0.8430
Epoch 2/5
25000/25000 [==============================] - 9s - loss: 0.2528 - acc: 0.8976 - val_loss: 0.3962 - val_acc: 0.8284
...

Result with Position Embedding:

Train on 25000 samples, validate on 25000 samples
Epoch 1/5
25000/25000 [==============================] - 9s - loss: 0.5179 - acc: 0.7183 - val_loss: 0.3540 - val_acc: 0.8413
Epoch 2/5
25000/25000 [==============================] - 9s - loss: 0.2880 - acc: 0.8786 - val_loss: 0.3464 - val_acc: 0.8447
...

It seems the peak accuracy is slightly higher than a single-layer LSTM, and Position Embedding improves accuracy and reduces overfitting.

Computational Complexity Analysis

As you can see, the computational cost of Attention is not low. In Self-Attention, you first perform three linear mappings on $\boldsymbol{X}$. This part is $O(n)$, comparable to a 1D convolution with kernel size 3. However, it also includes two matrix multiplications of the sequence with itself, both of which are $O(n^2)$. If the sequence is long enough, this complexity becomes difficult to accept.

This suggests that restricted versions of Attention are an important research area, and that combining Attention with CNNs and RNNs is likely the most balanced path forward.

Conclusion

Thanks to Google for providing such a wonderful case study, which has been an eye-opener and deepened our understanding of Attention. Google's work embodies the philosophy of "simplicity is the ultimate sophistication" and is a rare gem in NLP. I have tried to provide some insights here, and I hope it helps readers better understand Attention. I welcome any suggestions or criticisms.