A Simple Python Implementation of Gillespie Simulation

By 苏剑林 | June 07, 2018

Due to professional requirements, I needed to perform stochastic simulations of the master equation. Since I couldn't find a suitable Python implementation online, I wrote one myself and am sharing the source code. As for the Gillespie algorithm itself, I won't introduce it here; readers who need it will naturally understand, and those who don't are advised not to bother.

Source Code

In fact, the basic Gillespie simulation algorithm is very simple and easy to implement. Below is a reference example:

import numpy as np

class System:
    def __init__(self, num_elements):
        self.num_elements = num_elements
        self.reactions = []
    def add_reaction(self, rate, num_lefts, num_rights):
        assert len(num_lefts) == self.num_elements
        assert len(num_rights) == self.num_elements
        self.reactions.append([rate, np.array(num_lefts), np.array(num_rights)])
    def evolute(self, max_steps, init_nums):
        init_nums = np.array(init_nums)
        ts, nums = [0], [init_nums]
        for i in range(max_steps):
            propensities = []
            for rate, num_lefts, num_rights in self.reactions:
                p = rate
                for j in range(self.num_elements):
                    if num_lefts[j] > 0:
                        p *= init_nums[j] 
                propensities.append(p)
            propensities = np.array(propensities)
            p_sum = propensities.sum()
            if p_sum > 0:
                tau = np.random.exponential(1/p_sum)
                ts.append(ts[-1] + tau)
                r = np.random.rand() * p_sum
                idx = np.searchsorted(np.cumsum(propensities), r)
                init_nums = init_nums - self.reactions[idx][1] + self.reactions[idx][2]
                nums.append(init_nums)
            else:
                break
        return np.array(ts), np.array(nums)

Usage

For ease of use, I encapsulated the reactions. Now, you only need to provide the reaction equations to perform the simulation directly without additional programming operations. For instance, consider a simple gene expression model:

\begin{aligned} DNA &\xrightarrow{\quad 20\quad} DNA + m\\ m &\xrightarrow{\quad 2.5\quad} m + n\\ m &\xrightarrow{\,\quad 1\,\,\quad} \phi\\ n &\xrightarrow{\,\quad 1\,\,\quad} \phi \end{aligned}

Here $m, n$ respectively represent the number of mRNA and protein molecules, and $\phi$ is empty, meaning degradation or "creation from nothing". The first reaction can be simplified to $\phi \xrightarrow{\quad 20\quad} m$, so there are actually four reaction formulas for two types of substances $m, n$.

num_elements = 2 # mRNA: 0, protein: 1
system = System(num_elements)

# phi -> m
system.add_reaction(20, [0, 0], [1, 0])
# m -> m + n
system.add_reaction(2.5, [1, 0], [1, 1])
# m -> phi
system.add_reaction(1, [1, 0], [0, 0])
# n -> phi
system.add_reaction(1, [0, 1], [0, 0])

ts, nums = system.evolute(100000, [0, 0])

Then you can gather statistics and plot the results:

import matplotlib.pyplot as plt

plt.figure(figsize=(10, 5))
plt.plot(ts, nums[:, 1])
plt.xlabel('Time')
plt.ylabel('Protein Number')
plt.show()

plt.figure(figsize=(10, 5))
plt.hist(nums[2000:, 1], bins=50, density=True)
plt.xlabel('Protein Number')
plt.ylabel('Probability')
plt.show()

The results are:

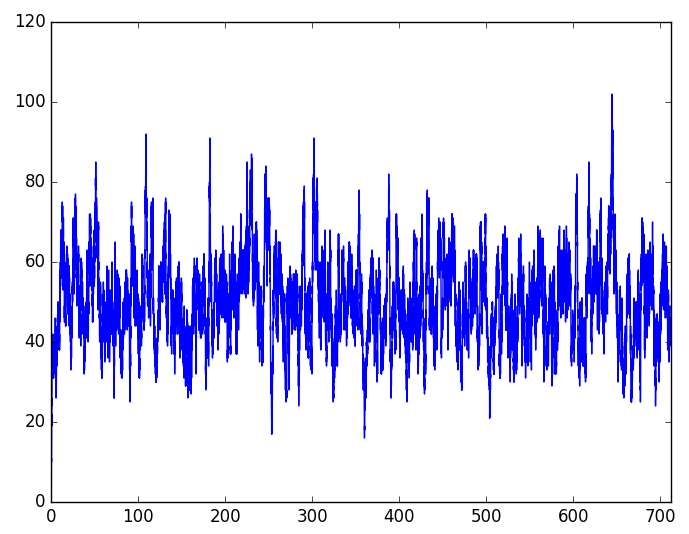
Change of protein over time (trajectory)

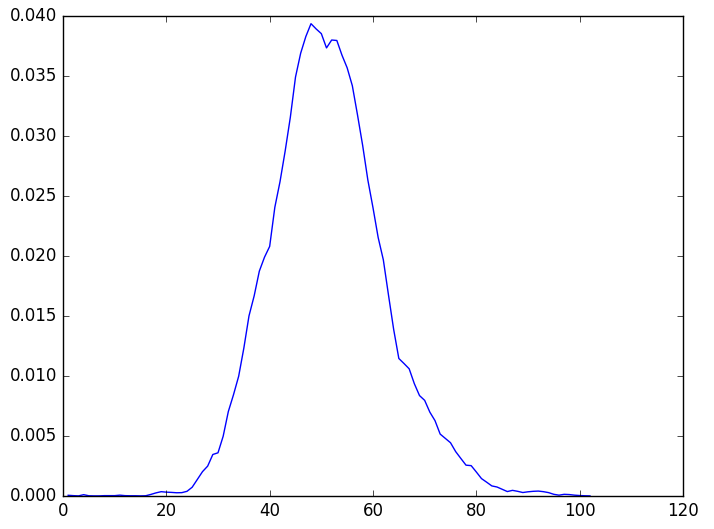
Statistical distribution of protein

If you still have any doubts or suggestions, you are welcome to continue the discussion in the comments section below.

Category: Physical Chemistry | Tags: Probability, Simulation, Stochastic, Master Equation