By 苏剑林 | October 31, 2019
In my opinion, among the major conferences, ICLR papers are usually the most interesting. This is because their topics and styles are generally relaxed, lively, and imaginative, often giving one the feeling of a wide-open "brainstorm." Therefore, after the submitted paper list for ICLR 2020 came out, I took some time to browse through them and indeed found many interesting works.
Among them, I discovered two papers that use the idea of denoising autoencoders to build generative models, namely "Learning Generative Models using Denoising Density Estimators" and "Annealed Denoising Score Matching: Learning Energy-Based Models in High-Dimensional Spaces". Since I am already familiar with the conventional approaches to generative models, this "unique" perspective piqued my interest. Upon closer reading, I found that their starting points are the same, but their specific implementations differ, and their final resolutions converge again—a beautiful instance of "multiple solutions to one problem." Thus, I have grouped these two papers together for a comparative analysis.
The fundamental starting point of both papers is the Denoising Autoencoder (DAE), or more precisely, they utilize the optimal solution of a denoising autoencoder:
Basic Result: If $x, \varepsilon \in \mathbb{R}^d$, with $x \sim p(x)$ and $\varepsilon \sim u(\varepsilon)$, where $u(\varepsilon) = \mathcal{N}(0, \sigma^2 I_d)$, then
\begin{equation}\begin{aligned}r(x)=&\, \mathop{\text{argmin}}_{r}\mathbb{E}_{x\sim p(x),\varepsilon\sim \mathcal{N}(0,\sigma^2 I_d)}\left[\Vert r(x + \varepsilon) - x\Vert^2\right] \\ =&\,x + \sigma^2 \nabla_x \,\log\hat{p}(x)\end{aligned}\label{eq:denoise}\end{equation}
Here $\hat{p}(x) = [p * u](x) = \int p(x-\varepsilon)u(\varepsilon) d\varepsilon = \int p(\varepsilon)u(x-\varepsilon) d\varepsilon$ refers to the convolution operation of the distributions $p(x)$ and $u(\varepsilon)$. Specifically, it represents the probability density of $x + \varepsilon$. In other words, if $p(x)$ represents the distribution of real images, then if we can sample from $\hat{p}(x)$, we obtain a batch of real images with added Gaussian noise.
The result in \eqref{eq:denoise} means that the optimal denoising autoencoder for additive Gaussian noise can be calculated explicitly, and the result is related to the gradient of the distribution. This result is very interesting and profound, and it is worth reflecting on further. For instance, Equation \eqref{eq:denoise} tells us that $r(x) - x$ is actually an estimate of the gradient of the (noisy) real distribution. With the gradient of the real distribution, we can do many things, especially those related to generative models.
Proof: In fact, the proof of \eqref{eq:denoise} is not difficult. Taking the variation of the objective gives:
\begin{equation}\begin{aligned}&\delta \iint p(x)u(\varepsilon)\left\Vert r(x + \varepsilon) - x\right\Vert_2^2 dx d\varepsilon\\ =&\delta \iint p(x)u(y-x)\left\Vert r(y) - x\right\Vert_2^2 dx dy\\ =&2\iint p(x)u(y-x)\left\langle r(y) - x, \delta r(y)\right\rangle dx dy\\ \end{aligned}\end{equation}Setting the integral to zero gives $\int p(x)u(y-x)(r(y) - x)dx = 0$, thus:
\begin{equation}r(y) = \frac{\int p(x)u(y-x)x dx}{\int p(x)u(y-x) dx}\end{equation}Substituting the expression $u(\varepsilon) = \frac{1}{(2\pi \sigma^2)^{d/2}}\exp\left(-\frac{\left\Vert\varepsilon\right\Vert_2^2}{2\sigma^2}\right)$, we obtain:
\begin{equation}r(y) = y + \sigma^2\nabla_y \log\left[p*u\right](y)\end{equation}
We first introduce the logic of "Learning Generative Models using Denoising Density Estimators". Following the usual practice of GANs and VAEs, we want to train a mapping $x = G(z)$ such that $z$ sampled from a prior distribution $q(z)$ is mapped to a real sample. In probabilistic terms, we wish to reduce the distance between $p(x)$ and the following $q(x)$:
\begin{equation}q(x) = \int q(z)\delta(x - G_{\theta}(z))dz\end{equation}To this end, a common optimization goal for GANs is to minimize $KL(q(x) \Vert p(x))$. This perspective can be referenced in "Unified Understanding of Generative Models via Variational Inference (VAE, GAN, AAE, ALI)" and "GAN Models from an Energy Perspective (II): GAN = 'Analysis' + 'Sampling'". However, since we previously estimated the gradient of $\hat{p}(x)$, we can change our target to minimizing $KL\left(\hat{q}(x)\big\Vert \hat{p}(x)\right)$.
For this purpose, we can perform the derivation:
\begin{equation}\begin{aligned}KL\left(\hat{q}(x)\big\Vert \hat{p}(x)\right)=&\int \hat{q}(x) \log \frac{\hat{q}(x)}{\hat{p}(x)}dx\\ =&\int q(x)u(\varepsilon) \log \frac{\hat{q}(x+\varepsilon)}{\hat{p}(x+\varepsilon)}dx d\varepsilon\\ =&\int q(z)\delta(x-G_{\theta}(z))u(\varepsilon) \log \frac{\hat{q}(x+\varepsilon)}{\hat{p}(x+\varepsilon)}dx d\varepsilon dz\\ =&\int q(z)u(\varepsilon) \log \frac{\hat{q}(G_{\theta}(z)+\varepsilon)}{\hat{p}(G_{\theta}(z)+\varepsilon)}d\varepsilon dz\\ =&\,\mathbb{E}_{z\sim q(z), \varepsilon\sim u(\varepsilon)}\big[\log \hat{q}(G_{\theta}(z)+\varepsilon) - \log \hat{p}(G_{\theta}(z)+\varepsilon)\big]\\ \end{aligned}\label{eq:dae-1}\end{equation}This objective requires us to obtain estimates for $\log\hat{p}(x)$ and $\log\hat{q}(x)$. We can construct two models $E_p(x)$ and $E_q(x)$ mapping from $\mathbb{R}^d \to \mathbb{R}$ using neural networks, and then minimize their respective objectives:
\begin{equation}\begin{aligned}\mathop{\text{argmin}}_{E_p}\mathbb{E}_{x\sim p(x),\varepsilon\sim \mathcal{N}(0,\sigma^2 I_d)}\left[\Vert \nabla_x E_p(x + \varepsilon) + \varepsilon\Vert^2\right]\\ \mathop{\text{argmin}}_{E_q}\mathbb{E}_{x\sim q(x),\varepsilon\sim \mathcal{N}(0,\sigma^2 I_d)}\left[\Vert \nabla_x E_q(x + \varepsilon) + \varepsilon\Vert^2\right] \end{aligned}\label{eq:e-grad}\end{equation}That is, using $\nabla_x E_p(x)+x$ and $\nabla_x E_q(x)+x$ as denoising autoencoders. According to the result \eqref{eq:denoise}, we have:
\begin{equation}\left\{\begin{aligned}\nabla_x E_p(x)+x=x+\sigma^2 \nabla_x \log \hat{p}(x)\\ \nabla_x E_q(x)+x=x+\sigma^2 \nabla_x \log \hat{q}(x)\end{aligned}\right. \quad\Rightarrow\quad \left\{\begin{aligned}E_p(x) = \sigma^2 \log \hat{p}(x) + C_1\\ E_q(x) = \sigma^2 \log \hat{q}(x) + C_2\end{aligned}\right.\end{equation}This means that, up to a constant, $E_p(x)$ is proportional to $\log \hat{p}(x)$ and $E_q(x)$ is proportional to $\log \hat{q}(x)$. Since the constants do not affect the optimization, we can substitute $E_p(x)$ and $E_q(x)$ into \eqref{eq:dae-1}, yielding:
\begin{equation}KL\left(\hat{q}(x)\big\Vert \hat{p}(x)\right)\sim\,\mathbb{E}_{z\sim q(z), \varepsilon\sim u(\varepsilon)}\big[E_q(G_{\theta}(z)+\varepsilon) - E_p(G_{\theta}(z)+\varepsilon)\big]\label{eq:dae-2}\end{equation}This provides a workflow for a generative model:
Select a prior distribution $q(z)$, initialize $G_{\theta}(z)$, and pre-compute $E_p(x)$. Execute the following three steps iteratively until convergence:
1. Select a batch of $z \sim q(z)$ and a batch of noise $\varepsilon \sim \mathcal{N}(0, \sigma^2 I_d)$; synthesize a batch of noisy fake samples $x = G_{\theta}(z) + \varepsilon$.
2. Use this batch of noisy fake samples to train $E_q(x)$.
3. Fix $E_p$ and $E_q$, and update $G_{\theta}$ for several steps using gradient descent based on \eqref{eq:dae-2}.
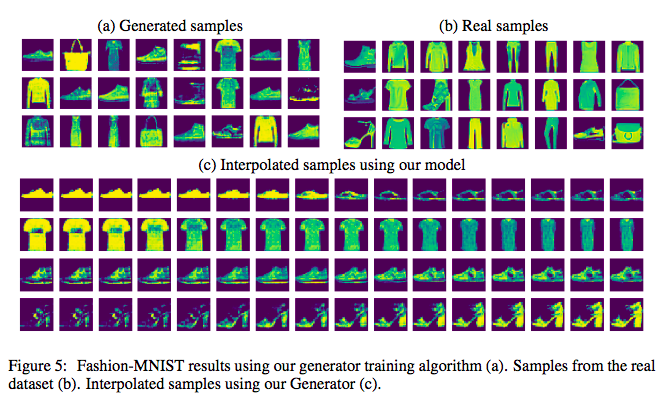
The experiments in this paper are relatively simple, only covering MNIST and Fashion MNIST, but they prove its feasibility:
Generation performance on Fashion MNIST
The other paper, "Annealed Denoising Score Matching: Learning Energy-Based Models in High-Dimensional Spaces," is even more direct. It is essentially a combination of the denoising autoencoder and the ideas in "GAN Models from an Energy Perspective (III): Generative Model = Energy Model".
Since \eqref{eq:denoise} has already provided us with $\nabla_x \log \hat{p}(x) = (r(x) - x) / \sigma^2$ (of course, the actual method in the paper doesn't use a neural network to fit $r(x)$ directly but instead uses a neural network to fit a scalar function, much like \eqref{eq:e-grad}, but this doesn't affect the core idea), this effectively helps us sample from $\hat{p}(x)$. Of course, the sampled images will have noise, so we need to pass the sampling results through $r(x)$ to denoise them, i.e.,
$$p(x) = \mathbb{E}_{x_{noise}\sim \hat{p}(x)} \big[\delta(x - r(x_{noise}))\big]$$
So specifically, how do we sample from $\hat{p}(x)$? Langevin equations! Since we already know $\nabla_x \log \hat{p}(x)$, the following Langevin equation:
\begin{equation}x_{t+1} = x_t + \frac{1}{2}\varepsilon \nabla_x\log\hat{p}(x) + \sqrt{\varepsilon}\alpha,\quad \alpha \sim \mathcal{N}(\alpha;0,1)\label{eq:sde}\end{equation}will have a distribution for the sequence $\{x_t\}$ that follows $\hat{p}(x)$ as $\varepsilon \to 0$ and $t \to \infty$. In other words, $\hat{p}(x)$ is the stationary distribution of this Langevin equation.
Consequently, the process of sampling from $\hat{p}(x)$ was solved by "Annealed Denoising Score Matching: Learning Energy-Based Models in High-Dimensional Spaces" in this straightforward (though in my view, perhaps less elegant) manner. Thus, after training the denoising autoencoder, a generative model is automatically obtained...
The overall process is:
1. Train a denoising autoencoder $r(x)$ to obtain $\nabla_x \hat{p}(x)$.
2. Use the iterative process \eqref{eq:sde} for sampling; the sampling results are a batch of noisy real samples.
3. Pass the sampling results from Step 2 into $r(x)$ to denoise them, producing noise-free samples.
Naturally, the paper contains many more details. The core trick of the paper is the use of an annealing technique to stabilize the training process and improve generation quality. However, I am not particularly interested in those details as I am mainly looking to learn new and interesting generative modeling ideas to broaden my horizons. Nevertheless, it must be said that despite being somewhat "brute-force," the generation results of this paper are quite competitive, showing very good performance on Fashion MNIST, CelebA, and CIFAR-10:
Generation performance on Fashion MNIST, CelebA, and CIFAR-10
This article introduced two similar papers submitted to ICLR 2020 which utilize denoising autoencoders to create generative models. Since I had not encountered this line of thinking before, I read and compared them with great interest.
Leaving aside the generation quality for a moment, I find them both quite enlightening and capable of sparking reflection (not just in CV, but also in NLP). For example, BERT's MLM pre-training method is essentially a denoising autoencoder as well. Is there a result similar to \eqref{eq:denoise} for it? Or conversely, can results similar to \eqref{eq:denoise} inspire us to construct new pre-training tasks, or perhaps clarify the underlying principles of the pre-train + fine-tune workflow?