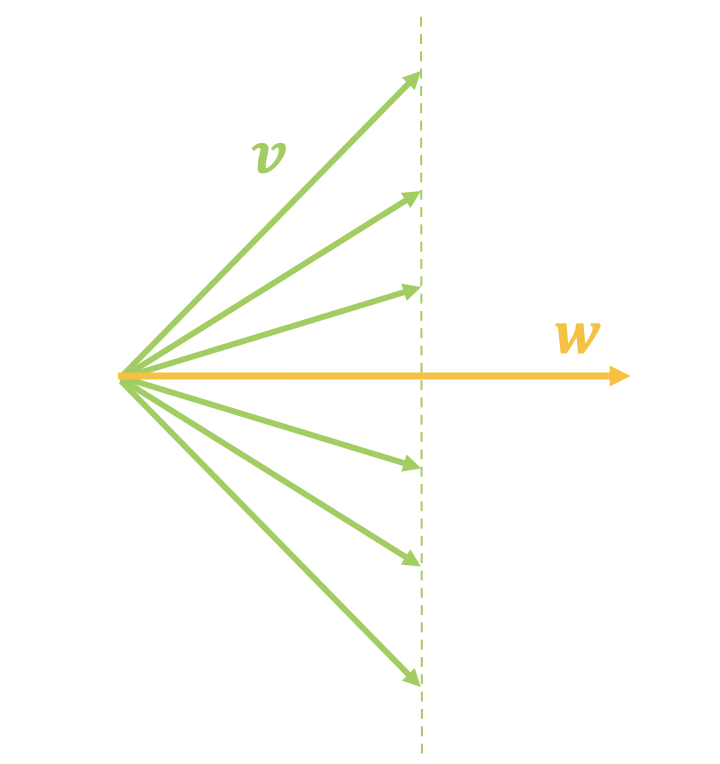
Vectors v with the same inner product with w can be very different
By 苏剑林 | December 01, 2019
Yesterday while browsing Arxiv, I discovered a paper from South Korea with a very straightforward title: "A Simple yet Effective Way for Improving the Performance of GANs". Upon opening it, I found the content to be very concise, proposing a method to strengthen the GAN discriminator that can lead to certain improvements in generation metrics.
The authors call this method "Cascading Rejection." I wasn't quite sure how to translate it, but Baidu Translate suggested "级联抑制" (Cascading Suppression/Rejection), which seems to fit the logic, so I will refer to it as such for now. I am introducing this method not because it is exceptionally powerful, but because its geometric meaning is very interesting and seems to offer some inspiration.
A GAN discriminator generally produces a fixed-length vector $\boldsymbol{v}$ through multiple layers of convolution followed by flattening or pooling. This vector is then used in an inner product with a weight vector $\boldsymbol{w}$ to obtain a scalar score (ignoring bias terms and activation functions for simplicity):
\begin{equation}D(\boldsymbol{x})=\langle \boldsymbol{v},\boldsymbol{w}\rangle\end{equation}In other words, $\boldsymbol{v}$ is used as the representation of the input image, and the degree of "realness" of the image is judged by the magnitude of the inner product between $\boldsymbol{v}$ and $\boldsymbol{w}$.
However, $\langle \boldsymbol{v},\boldsymbol{w}\rangle$ only depends on the projection component of $\boldsymbol{v}$ onto $\boldsymbol{w}$. In other words, when $\langle \boldsymbol{v},\boldsymbol{w}\rangle$ and $\boldsymbol{w}$ are fixed, $\boldsymbol{v}$ can still vary significantly, as shown in the left figure below.

Vectors v with the same inner product with w can be very different
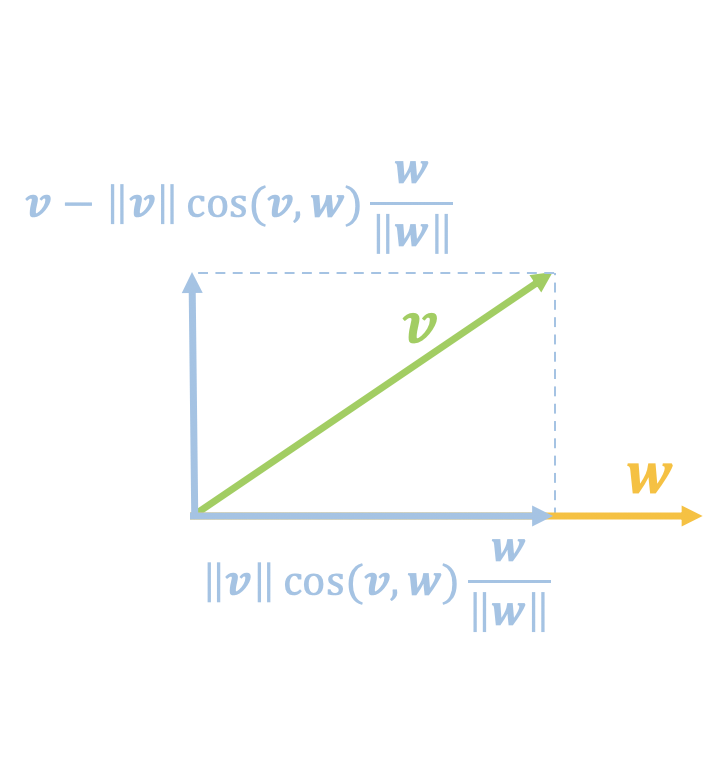
Projection component and perpendicular component of v
If we believe an image is "real" when $\langle \boldsymbol{v},\boldsymbol{w}\rangle$ equals a certain value, the problem is that since $\boldsymbol{v}$ can vary so much, does every $\boldsymbol{v}$ truly represent a real image? Not necessarily. This reflects the limitation of scoring via inner product: it only considers the projection component on $\boldsymbol{w}$ and ignores the perpendicular component (as shown in the right figure above):
\begin{equation}\boldsymbol{v}-\Vert \boldsymbol{v}\Vert \cos(\boldsymbol{v},\boldsymbol{w}) \frac{\boldsymbol{w}}{\Vert \boldsymbol{w}\Vert}=\boldsymbol{v}- \frac{\langle\boldsymbol{v},\boldsymbol{w}\rangle}{\Vert \boldsymbol{w}\Vert^2}\boldsymbol{w}\end{equation}Given this, a natural idea is: can we use another parameter vector to perform classification again on this perpendicular component? Clearly, we can. Furthermore, this second classification of the perpendicular component will also result in a new perpendicular component, so this process can be iterated:
\begin{equation} \left\{ \begin{aligned} &\boldsymbol{v}_1=\boldsymbol{v}\\ &D_1(\boldsymbol{x})=\langle \boldsymbol{v}_1,\boldsymbol{w}_1\rangle\\ &\boldsymbol{v}_2 = \boldsymbol{v}_1- \frac{\langle\boldsymbol{v}_1,\boldsymbol{w}_1\rangle}{\Vert \boldsymbol{w}_1\Vert^2}\boldsymbol{w}_1\\ &D_2(\boldsymbol{x})=\langle \boldsymbol{v}_2,\boldsymbol{w}_2\rangle\\ &\boldsymbol{v}_3 = \boldsymbol{v}_2- \frac{\langle\boldsymbol{v}_2,\boldsymbol{w}_2\rangle}{\Vert \boldsymbol{w}_2\Vert^2}\boldsymbol{w}_2\\ &D_3(\boldsymbol{x})=\langle \boldsymbol{v}_3,\boldsymbol{w}_3\rangle\\ &\boldsymbol{v}_4 = \boldsymbol{v}_3- \frac{\langle\boldsymbol{v}_3,\boldsymbol{w}_3\rangle}{\Vert \boldsymbol{w}_3\Vert^2}\boldsymbol{w}_3\\ &\qquad\vdots\\ &D_N(\boldsymbol{x})=\langle \boldsymbol{v}_N,\boldsymbol{w}_N\rangle\\ \end{aligned} \right. \end{equation}Essentially, the core idea of the original paper has been explained; the rest involves some implementation details. First, since there are now $N$ scores $D_1(\boldsymbol{x}),D_2(\boldsymbol{x}),\dots,D_N(\boldsymbol{x})$, each score can be applied to the discriminator's loss (either directly using hinge loss or with a sigmoid activation followed by cross-entropy). Finally, a weighted average of these $N$ losses is taken as the final discriminator loss. This alone can bring performance improvements to the GAN. The authors also extended this to CGANs and obtained good results.
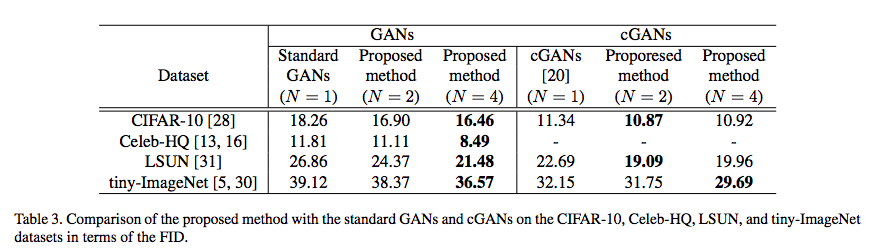
Experimental results of the proposed GAN technique
Compared to the experimental results, I believe the deeper significance of this technique is more worthy of attention. In principle, this idea could be applied to general classification problems, not just GANs. By iteratively incorporating perpendicular components into the prediction, we can consider the parameters $\boldsymbol{w}_1,\boldsymbol{w}_2,\dots,\boldsymbol{w}_N$ as representing $N$ different perspectives, and each classification corresponds to a judgment from a different viewpoint.
Thinking about this, I am reminded of Hinton's Capsule. Although the form is different, the underlying intention seems similar. Capsules aim to represent an entity with a vector rather than a scalar. This "Cascading Rejection" also provides multiple classification results through continuous perpendicular decomposition. In other words, to determine if a vector belongs to a class, it must provide multiple scores rather than just one. This also has the flavor of "using vectors rather than scalars."
Regrettably, when I performed a simple experiment (on CIFAR-10) using this approach, I found that the classification accuracy on the validation set decreased slightly (note that this does not contradict the GAN results; GAN performance improves because it increases the difficulty for the discriminator, whereas supervised classification models do not benefit from increased discrimination difficulty). However, on the bright side, the degree of overfitting decreased (i.e., the gap between training and validation accuracy narrowed). Of course, my experiment was too simple to draw a rigorous conclusion. Nevertheless, I still feel that due to its distinct geometric meaning, this technique is worth further consideration.
This article introduced a technique with distinct geometric significance for improving GAN performance and further discussed its potential value.
Original address of this article: https://kexue.fm/archives/7105