RealFormer: Moving Residuals to the Attention Matrix

By 苏剑林 | December 24, 2020

As is well known, Layer Normalization is one of the crucial components of the Transformer model. Its usage generally falls into two categories: PostLN and PreLN. The paper "On Layer Normalization in the Transformer Architecture" provides a detailed analysis of both. Simply put, PreLN is more friendly to gradient descent, converges faster, and is more robust to training hyperparameters like learning rate. In almost every respect, it seems superior, except for one significant drawback: the performance of PreLN always seems slightly worse than PostLN. Recently, a paper from Google titled "RealFormer: Transformer Likes Residual Attention" proposed the RealFormer design, successfully bridging this gap. This allows the model to possess the optimization friendliness of PreLN while achieving better performance than PostLN, truly offering the best of both worlds.

Form

RealFormer stands for "Residual Attention Layer Transformer." As the name suggests, it places the residual connection inside the Attention mechanism.

Regarding the name, there is a small anecdote. When this blog post was first drafted, RealFormer was actually named Informer, standing for "Residual Attention Transformer," and the original paper was titled "Informer: Transformer Likes Informed Attention". Obviously, it was hard to guess the full name from "Informer," and I previously criticized Google's somewhat stiff and arbitrary naming. A day later, I discovered it had been renamed RealFormer, so I updated accordingly. It is unclear whether the authors saw my critique or if the rename was due to its name clashing with another paper released just days earlier, "Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting."

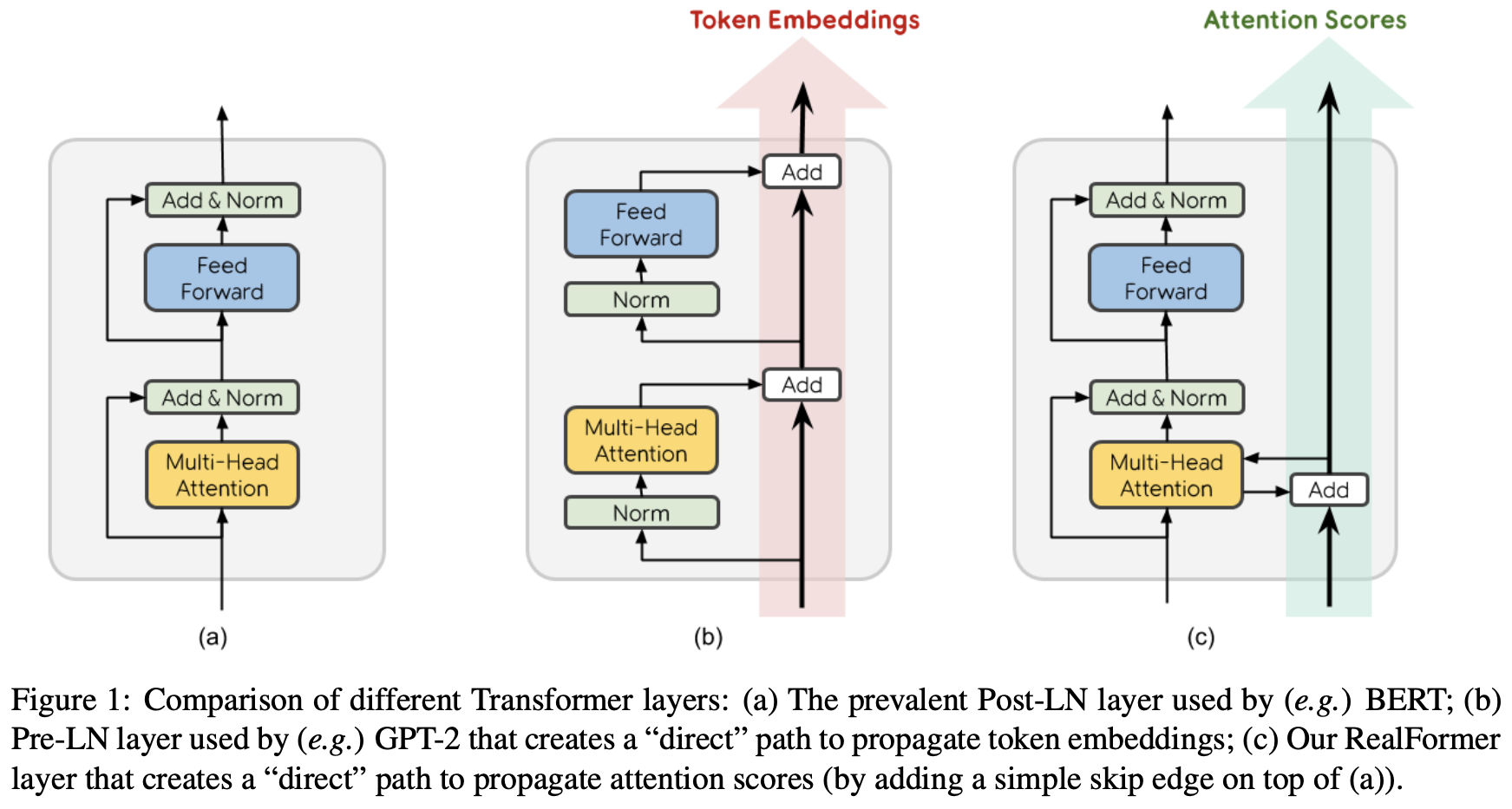
Schematic of PostLN, PreLN, and RealFormer structures

Returning to the model, as shown in the figure above, RealFormer primarily moves the residual connection to the Attention matrix while maintaining the overall PostLN structure. Thus, it retains the performance of PostLN while integrating the friendliness of residual connections. Specifically, where the Attention in the $n$-th layer was originally:

It has now been changed to:

And that is essentially it.

Experiments

Of course, it's impossible to end the discussion there; we must look at the experimental results. But in terms of modifications, it really is that simple. The original paper conducted extensive experiments, and basically all results indicate the following performance ranking:

It seems that PostLN might finally be ready for retirement. Some experimental results are shown below:

Comparison of MLM accuracy

SQuAD evaluation comparison

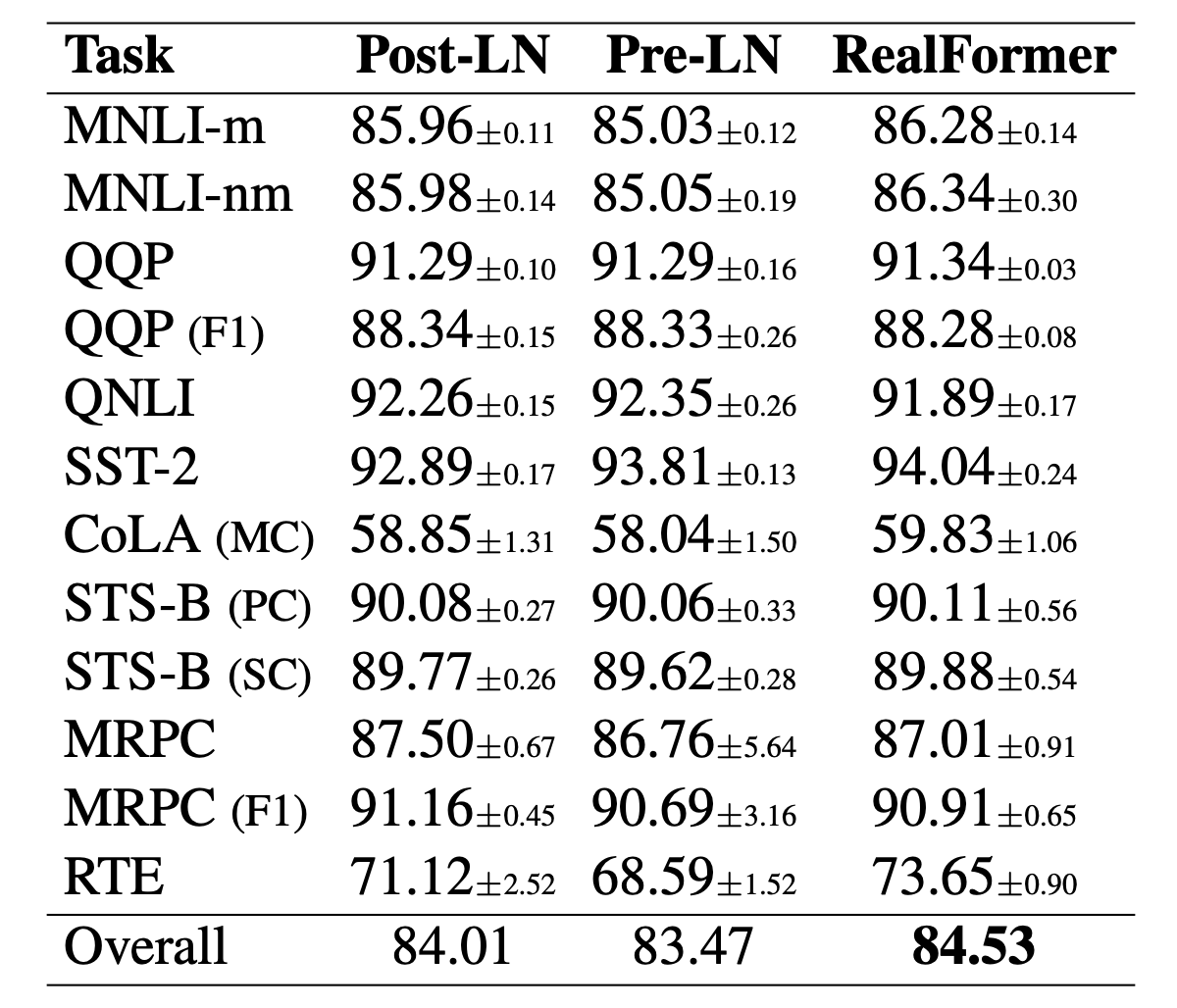
GLUE evaluation comparison

Effect comparison across different training steps

It is worth highlighting the first and fourth figures. From the first figure, we can see that for the RealFormer structure, increasing the model scale (from "large" to "xlarge") leads to a significant performance improvement. In contrast, the ALBERT paper previously mentioned that increasing BERT's model size does not yield significant benefits. Combining these two observations suggests this might be an issue with PostLN rather than an inherent problem with BERT, and switching to RealFormer can improve this. From the fourth figure, we see that training the RealFormer structure for 500,000 steps achieves results equivalent to training PostLN for 1,000,000 steps, indicating that RealFormer has very high training efficiency.

In addition to these experiments, the paper also provides comparisons across different learning rates and Dropout ratios, showing that RealFormer is indeed quite robust to these parameters. The original paper also analyzed the distribution of Attention scores, showing that the results produced by RealFormer are more reasonable.

Analysis

In this section, we provide a simple analysis of RealFormer.

It is not difficult to understand why RealFormer is more friendly to gradient descent. The design $\boldsymbol{A}_n=\frac{\boldsymbol{Q}_n\boldsymbol{K}_n^{\top}}{\sqrt{d_k}} + \boldsymbol{A}_{n-1}$ provides a direct path, allowing the Attention of the first layer to reach the last layer directly, naturally eliminating the risk of gradient vanishing. In contrast, PostLN has a structure of $\text{LayerNorm}(x + f(x))$. While $x+f(x)$ seemingly prevents gradient vanishing, the $\text{LayerNorm}$ step reintroduces the risk. This results in small gradients for earlier layers and large gradients for later layers in the initial stages. If a large learning rate is used, the later layers easily collapse; if a small learning rate is used, the earlier layers do not learn well. Thus, PostLN is harder to train and requires small learning rates combined with a warmup phase.

So, if PreLN improves gradient conditions, why is it still inferior to PostLN? My guess is that PreLN takes the form $x+f(x)$ at every step, which by the last layer becomes $x + f_1(x) + f_2(x) + \cdots + f_n(x)$. This layer-by-layer accumulation can lead to very large values and variances, necessitating the mandatory addition of a Layer Norm at the final stage to stabilize the output. Thus, while PreLN improves the gradient situation, its design includes some inherent instabilities, which might be why its performance is slightly worse.

In fact, someone noticed very early on that this characteristic of residuals causes instability. When I was researching GANs, I found that the implementation in the paper "Which Training Methods for GANs do actually Converge?" replaced $x + f(x)$ with $x + 0.1 f(x)$. Inspired by their implementation, I tried replacing $x + f(x)$ with $x + \alpha f(x)$, where $\alpha$ is a trainable scalar parameter initialized to 0, which also achieved good results. Earlier this year, the paper "ReZero is All You Need: Fast Convergence at Large Depth" formally proposed this method, naming it ReZero. The experiments therein showed that ReZero allows the complete removal of Layer Norm. Unfortunately, the ReZero paper did not conduct more experiments on Transformers, and RealFormer did not compare its effects with ReZero.

Readers might argue: If PreLN has issues, doesn't RealFormer's $\boldsymbol{A}_n=\frac{\boldsymbol{Q}_n\boldsymbol{K}_n^{\top}}{\sqrt{d_k}} + \boldsymbol{A}_{n-1}$ suffer from the same accumulation problem? If we only look at $\boldsymbol{A}$, then yes, that problem exists. But don't forget that $\boldsymbol{A}$ is normalized by the softmax function before participating in operations. In other words, the model has a built-in normalization function for matrix $\boldsymbol{A}$, so it does not suffer from numerical divergence. On the contrary, as the number of layers increases, the accumulation of $\boldsymbol{A}$ makes the absolute values of its elements potentially larger, causing the Attention to gradually trend towards a one-hot form, which results in gradient vanishing in later layers. However, remember that we previously said PostLN has small gradients in earlier layers and large ones in later layers; here, the gradients of the later layers are also reduced, making the layers more synchronized and thus easier to optimize. On the other hand, the probability values of the Attention might show a trend of convergence, meaning the Attention patterns become increasingly stable, which brings a regularization effect similar to the parameter sharing in ALBERT. This may be beneficial for model performance. Intuitively, using the RealFormer structure for adaptive layer depth improvements like FastBERT might yield better results because the convergence trend in RealFormer's Attention aligns better with the design principles of FastBERT.

Furthermore, we can interpret RealFormer as still using a conventional residual structure, but applying it only to $\boldsymbol{Q}$ and $\boldsymbol{K}$, and not to $\boldsymbol{V}$:

To some extent, this is equivalent to $\boldsymbol{A}_n=\frac{\boldsymbol{Q}_n\boldsymbol{K}_n^{\top}}{\sqrt{d_k}} + \boldsymbol{A}_{n-1}$, whereas PreLN is equivalent to adding residuals to $\boldsymbol{Q}, \boldsymbol{K},$ and $\boldsymbol{V}$. Why is $\boldsymbol{V}$ "not worth" a residual? From recent improvements in relative position encoding, I have noticed a common trend: removing the bias from $\boldsymbol{V}$. For example, in the relative position encoding of NEZHA, the encoding is applied simultaneously to the Attention matrix (i.e., $\boldsymbol{Q}, \boldsymbol{K}$) and $\boldsymbol{V}$. However, in the newer relative position encodings of XLNET and T5, it is only applied to the Attention matrix. Therefore, it seems that removing unnecessary bias from $\boldsymbol{V}$ is a better choice, and RealFormer reflects this once again.

Summary

This article introduced RealFormer, a new design for Transformers from Google, and provided my own analysis and reflections. Experimental results show that RealFormer simultaneously possesses the advantages of PostLN and PreLN and even outperforms both, making it a valuable improvement to use.