By 苏剑林 | Feb 16, 2021
The $\mathcal{O}(n^2)$ complexity of standard Attention is truly a headache for researchers. Recently, in the blog post "Performer: Linearizing Attention Complexity with Random Projections", we introduced Google's Performer model, which transforms standard Attention into linear Attention via random projections. Coincidentally, a paper titled "Nyströmformer: A Nyström-Based Algorithm for Approximating Self-Attention" was released on Arxiv for AAAI 2021, proposing another scheme to linearize standard Attention from a different perspective.
This scheme is "Nyström-Based," which, as the name suggests, utilizes the Nyström method to approximate standard Attention. However, frankly speaking, before seeing this paper, I had never heard of the Nyström method. Looking through the entire paper, it is filled with matrix decomposition derivations that seemed somewhat confusing at first glance. Interestingly, although the author's derivation is complex, I found that the final result can be understood through a relatively simpler approach. I have organized my understanding of Nyströmformer here for your reference.
If you are not yet familiar with linear Attention, it is recommended to first read "Exploring Linear Attention: Does Attention Need a Softmax?" and "Performer: Linearizing Attention Complexity with Random Projections". In general, linear Attention reduces the complexity of Attention through the associative property of matrix multiplication.
Standard Scaled-Dot Attention written in matrix form is (sometimes the exponent part includes an additional scaling factor, which we will not write explicitly here):
\begin{equation}Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = softmax\left(\boldsymbol{Q}\boldsymbol{K}^{\top}\right)\boldsymbol{V}\end{equation}Here $\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V}\in\mathbb{R}^{n\times d}$ (corresponding to Self Attention). Additionally, all "softmax" operations in this article are normalized over the second dimension of the matrix.
In the above formula, $\boldsymbol{Q}\boldsymbol{K}^{\top}$ must be calculated first before the softmax can be applied, which prevents us from using the associative property of matrix multiplication. Since $\boldsymbol{Q}\boldsymbol{K}^{\top}$ consists of $n^2$ dot products of vectors, both time and space complexity are $\mathcal{O}(n^2)$.
A naive approach to linear Attention is:
\begin{equation}\left(\phi(\boldsymbol{Q})\varphi(\boldsymbol{K})^{\top}\right)\boldsymbol{V}=\phi(\boldsymbol{Q})\left(\varphi(\boldsymbol{K})^{\top}\boldsymbol{V}\right)\end{equation}where $\phi, \varphi$ are activation functions with non-negative output values. For comparison, the normalization factor is not explicitly written above, highlighting only the main computational part. The complexity of the left side is still $\mathcal{O}(n^2)$; however, because matrix multiplication is associative, we can calculate the multiplication of the last two matrices first, thereby reducing the overall complexity to $\mathcal{O}(n)$.
The above equation directly defines Attention as the product of two matrices to exploit associativity. One can also (approximately) transform standard Attention into matrix products to use associativity, as seen in the Performer mentioned in the next section; furthermore, the matrices being multiplied do not necessarily have to be only two. For example, Nyströmformer, which we are introducing, represents attention as the product of three matrices.
Performer uses random projections to find matrices $\tilde{\boldsymbol{Q}},\tilde{\boldsymbol{K}}\in\mathbb{R}^{n\times m}$ such that $e^{\boldsymbol{Q}\boldsymbol{K}^{\top}}\approx \tilde{\boldsymbol{Q}}\tilde{\boldsymbol{K}}^{\top}$ in the softmax. In this way, standard Attention can be approximated as the linear Attention mentioned in the previous section. Details can be found in the blog post "Performer: Linearizing Attention Complexity with Random Projections".
Readers familiar with SVMs and kernel methods might realize this is essentially the idea of a kernel function—that is, the kernel function of two vectors in a low-dimensional space can be mapped to the inner product of two vectors in a high-dimensional space. It can also be linked to LSH (Locality Sensitive Hashing).
In this section, we start from a simple dual-softmax form of linear Attention and gradually seek a linear Attention that is closer to standard Attention, eventually arriving at Nyströmformer.
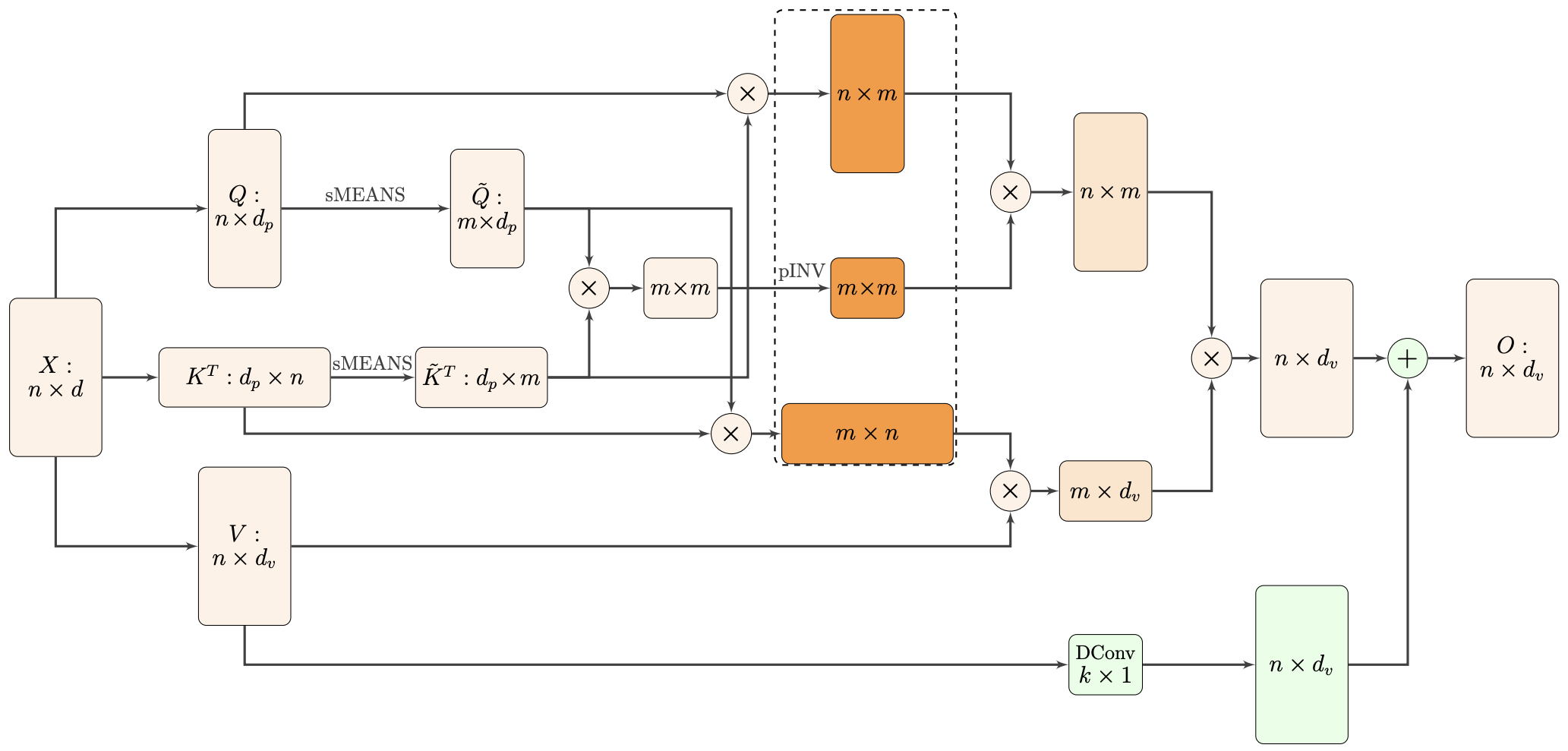
Nyströmformer architecture diagram. Readers can refer back to this diagram after reading the following sections.
In the article "Exploring Linear Attention: Does Attention Need a Softmax?", we mentioned an interesting linear Attention scheme that uses a dual softmax to construct the Attention matrix:
\begin{equation}\left(softmax(\boldsymbol{Q}) softmax\left(\boldsymbol{K}^{\top}\right)\right)\boldsymbol{V}=softmax(\boldsymbol{Q})\left(softmax\left(\boldsymbol{K}^{\top}\right)\boldsymbol{V}\right)\label{eq:2sm}\end{equation}It can be proven that an Attention matrix constructed this way automatically satisfies normalization requirements. One must admit this is a simple and elegant linear Attention scheme.
However, applying softmax directly to $\boldsymbol{Q}$ and $\boldsymbol{K}^{\top}$ seems a bit strange; it feels odd to apply softmax without a prior similarity (inner product) comparison. To address this, Nyströmformer first treats $\boldsymbol{Q}$ and $\boldsymbol{K}$ as $n$ vectors of dimension $d$ and clusters them into $m$ classes to obtain matrices $\tilde{\boldsymbol{Q}},\tilde{\boldsymbol{K}}\in\mathbb{R}^{m\times d}$ consisting of $m$ cluster centers. We can then define Attention via the following formula:
\begin{equation}\left(softmax\left(\boldsymbol{Q}\tilde{\boldsymbol{K}} ^{\top}\right)softmax\left(\tilde{\boldsymbol{Q}}\boldsymbol{K}^{\top}\right)\right)\boldsymbol{V} = softmax\left(\boldsymbol{Q} \tilde{\boldsymbol{K}}^{\top}\right)\left(softmax\left(\tilde{\boldsymbol{Q}}\boldsymbol{K}^{\top}\right)\boldsymbol{V}\right)\label{eq:2sm2}\end{equation}We will discuss the clustering process later. Now, the object of the softmax is the result of inner products, which has a distinct physical meaning. Thus, the above equation can be considered more reasonable than Eq. $\eqref{eq:2sm}$. If we select a relatively small $m$, the complexity of the right side linearly depends on $n$, making it a linear Attention.
Purely from the perspective of improving Eq. $\eqref{eq:2sm}$, Eq. $\eqref{eq:2sm2}$ has already achieved the goal. However, Nyströmformer does not stop there; it hopes the linearized result will be even closer to standard Attention. Observing that the attention matrix $softmax\left(\boldsymbol{Q}\tilde{\boldsymbol{K}}^{\top}\right)softmax\left(\tilde{\boldsymbol{Q}}\boldsymbol{K}^{\top}\right)$ in Eq. $\eqref{eq:2sm2}$ is an $n\times m$ matrix multiplied by an $m\times n$ matrix, to fine-tune the result without adding excessive complexity, we can consider inserting an $m\times m$ matrix $\boldsymbol{M}$ in the middle:
\begin{equation}softmax\left(\boldsymbol{Q}\tilde{\boldsymbol{K}} ^{\top}\right) \,\boldsymbol{M}\, softmax\left(\tilde{\boldsymbol{Q}}\boldsymbol{K}^{\top}\right)\end{equation}How should $\boldsymbol{M}$ be chosen? A reasonable requirement is that when $m=n$, it should be exactly equivalent to standard Attention. In this case, $\tilde{\boldsymbol{Q}}=\boldsymbol{Q}, \tilde{\boldsymbol{K}}=\boldsymbol{K}$, which implies:
\begin{equation}\boldsymbol{M} = \left(softmax\left(\boldsymbol{Q}\boldsymbol{K}^{\top}\right)\right)^{-1} = \left(softmax\left(\tilde{\boldsymbol{Q}}\tilde{\boldsymbol{K}}^{\top}\right)\right)^{-1}\end{equation}For a general $m$, $\left(softmax\left(\tilde{\boldsymbol{Q}}\tilde{\boldsymbol{K}}^{\top}\right)\right)^{-1}$ is precisely an $m\times m$ matrix, so choosing it as $\boldsymbol{M}$ is at least reasonable in terms of matrix operations. Based on the special case of $m=n$, we "boldly" conjecture that choosing it as $\boldsymbol{M}$ will make the new Attention mechanism closer to standard Attention. Thus, Nyströmformer ultimately chooses:
\begin{equation}softmax\left(\boldsymbol{Q}\tilde{\boldsymbol{K}} ^{\top}\right) \, \left(softmax\left(\tilde{\boldsymbol{Q}}\tilde{\boldsymbol{K}}^{\top}\right)\right)^{-1} \, softmax\left(\tilde{\boldsymbol{Q}}\boldsymbol{K}^{\top}\right)\end{equation}As an Attention matrix, it is the product of three small matrices. Therefore, through the associativity of matrix multiplication, it can be converted into linear Attention.
However, one theoretical detail needs to be addressed: the above formula involves matrix inversion, and $softmax\left(\tilde{\boldsymbol{Q}}\tilde{\boldsymbol{K}}^{\top}\right)$ might not be invertible. Of course, in practice, the probability of a real square matrix being non-invertible is almost zero (non-invertibility means the determinant is strictly zero; from a probabilistic standpoint, not being zero is much more likely). Thus, this can usually be ignored in experiments. Theoretically, however, it must be refined. This is simple: if the matrix is non-invertible, replace the inverse with the "pseudoinverse" (denoted as $^{\dagger}$), which exists for any matrix and equals the inverse if the matrix is invertible.
Therefore, the final Attention matrix form for Nyströmformer is:
\begin{equation}softmax\left(\boldsymbol{Q}\tilde{\boldsymbol{K}} ^{\top}\right) \, \left(softmax\left(\tilde{\boldsymbol{Q}}\tilde{\boldsymbol{K}}^{\top}\right)\right)^{\dagger} \, softmax\left(\tilde{\boldsymbol{Q}}\boldsymbol{K}^{\top}\right)\label{eq:2sm3}\end{equation}Theoretically, Eq. $\eqref{eq:2sm3}$ has achieved its goal. However, in practice, some details need to be handled, such as how to compute the pseudoinverse. The pseudoinverse, also called the generalized inverse or Moore-Penrose inverse, is standardly computed via SVD. Let the SVD decomposition of matrix $\boldsymbol{A}$ be $\boldsymbol{U} \boldsymbol{\Lambda} \boldsymbol{V}^{\top}$; then its pseudoinverse is:
\begin{equation}\boldsymbol{A}^{\dagger} = \boldsymbol{V} \boldsymbol{\Lambda}^{\dagger} \boldsymbol{U}^{\top}\end{equation}where the pseudoinverse of the diagonal matrix $\boldsymbol{\Lambda}$, denoted $\boldsymbol{\Lambda}^{\dagger}$, is obtained by taking the reciprocal of all non-zero values on its diagonal. While SVD is theoretically easy to understand, its calculation is expensive and it is not easy to compute gradients, making it a non-ideal way to implement pseudoinverse.
Nyströmformer uses an iterative approximation method for the inverse. Specifically, it employs the iterative algorithm from the paper "Chebyshev-type methods and preconditioning techniques":
If the initial matrix $\boldsymbol{V}_0$ satisfies $\Vert \boldsymbol{I} - \boldsymbol{A} \boldsymbol{V}_0\Vert < 1$, then for the following iterative format: \begin{equation}\begin{aligned} \boldsymbol{V}_{n+1} =& \,\left[\boldsymbol{I} + \frac{1}{4}\left(\boldsymbol{I} - \boldsymbol{V}_n \boldsymbol{A}\right)\left(3 \boldsymbol{I} - \boldsymbol{V}_n \boldsymbol{A}\right)^2\right] \boldsymbol{V}_n \\ =& \,\frac{1}{4} \boldsymbol{V}_n (13 \boldsymbol{I} − \boldsymbol{A} \boldsymbol{V}_n (15 \boldsymbol{I} − \boldsymbol{A} \boldsymbol{V}_n (7 \boldsymbol{I} − \boldsymbol{A} \boldsymbol{V}_n))) \end{aligned}\end{equation} the limit $\lim\limits_{n\to\infty} \boldsymbol{V}_n = \boldsymbol{A}^{\dagger}$ holds.
Here $\Vert\cdot\Vert$ can be any matrix norm. A simple initial value satisfying the condition is:
\begin{equation}\boldsymbol{V}_0 = \frac{\boldsymbol{A}^{\top}}{\Vert\boldsymbol{A}\Vert_1 \Vert\boldsymbol{A}\Vert_{\infty}} = \frac{\boldsymbol{A}^{\top}}{\left(\max\limits_j\sum\limits_i |A_{i,j}|\right)\left(\max\limits_i\sum\limits_j |A_{i,j}|\right)}\end{equation}In the Nyströmformer paper, the authors directly use the aforementioned initial values and iterative format, using the result of 6 iterations as a substitute for $\boldsymbol{A}^{\dagger}$. While 6 iterations might seem like a lot, since the $m$ chosen in the paper is small (the paper uses 64), the iteration process only involves matrix multiplication, so the computational burden is not too great. Furthermore, since it only involves multiplication, computing gradients is straightforward. Thus, the pseudoinverse problem is solved. The paper abbreviated this iterative process as pINV.
Another issue to solve is the choice of clustering method. A straightforward idea is to use K-Means. However, like the pseudoinverse problem, when designing a model, one must consider both forward calculation and backward gradient propagation. K-Means involves $\mathop{\text{argmin}}$ operations, which do not have meaningful gradients. "Softening" it to embed it into the model would essentially lead to the "dynamic routing" process of Capsule Networks, as discussed in "Another New Year's Eve Feast: From K-Means to Capsule". The main issue with this is that K-Means is an iterative process requiring several steps to ensure effectiveness, which significantly increases computation—making it less than ideal.
Nyströmformer chooses a very simple solution: assuming the sequence length $n$ is an integer multiple of $m$ (if not, pad with zero vectors), take the average of every $n/m$ vectors in $\boldsymbol{Q}, \boldsymbol{K}$ as each vector in $\tilde{\boldsymbol{Q}}, \tilde{\boldsymbol{K}}$. This operation is called Adaptive Average Pooling (referred to in the paper as Segment-Means, or sMEANS for short). It is a pooling method that uses an adaptive window size to ensure the pooled feature matrix has a fixed shape. Nyströmformer's experiments show that complex clustering methods are unnecessary; this simple adaptive pooling achieves very competitive results. Moreover, they only need $m=64$ (roughly the same size as the original $d$), which is much better than Performer, which requires an $m$ several times larger than $d$.
However, a significant disadvantage of adaptive pooling is that it "blurs" information from each interval, making it impossible to prevent future info leakage. Consequently, it cannot be used for autoregressive generation (like language models or Seq2Seq decoders), which is a common drawback of models using pooling tech.
Here we summarize the experimental results of Nyströmformer and share some personal thoughts and reflections.
Perhaps limited by computational power, the experiments in the original paper were not exceptionally extensive. They mainly replaced standard Attention with Nyströmformer in small and base versions of BERT for comparative experiments. The results are shown in the two figures below. One shows pre-training performance; interestingly, Nyströmformer actually outperformed standard Attention on the MLM task. The other shows fine-tuning effects on downstream tasks, demonstrating that it remains competitive with standard Attention (i.e., BERT).
Performance of Nyströmformer on pre-training tasks (MLM and SOP)
Downstream task fine-tuning results for Nyströmformer
However, the original paper did not compare Nyströmformer's effectiveness with similar models, providing only the complexity comparison chart below. Therefore, it is harder to see Nyströmformer's relative competitiveness:
Comparison of time and space complexity for different models
Overall, Nyströmformer's approach to approximating and linearizing standard Attention is quite novel and worth studying. However, the handling of the pseudoinverse feels slightly unnatural; this part could be a point for future improvement—if it could be done without approximation, it would be almost perfect. Additionally, how to quantitatively estimate the error between Nyströmformer and standard Attention is an interesting theoretical problem.
From the experiments, Nyströmformer appears competitive compared to standard Attention, particularly with its MLM results, showing its potential. Furthermore, as mentioned earlier, the inclusion of pooling makes Nyströmformer unable to perform autoregressive generation, which is a notable disadvantage. I haven't thought of a good way to remedy this yet.
Compared to Performer, Nyströmformer eliminates randomness in the linearization process. Performer achieves linearization through random projections, which inherently introduces randomness. For some perfectionist readers, this randomness might be unacceptable, whereas Nyströmformer is deterministic, which counts as a highlight.
Some readers might still want to learn about the Nyström method. To understand the Nyström method, one first needs a basic understanding of CUR decomposition of a matrix.
Most have heard of SVD decomposition, formulated as $\boldsymbol{A}=\boldsymbol{U} \boldsymbol{\Lambda} \boldsymbol{V}^{\top}$, where $\boldsymbol{U},\boldsymbol{V}$ are orthogonal matrices and $\boldsymbol{\Lambda}$ is diagonal. Note that $\boldsymbol{U},\boldsymbol{V}$ being orthogonal means they are dense. When $\boldsymbol{A}$ is very large, the computational and storage costs of SVD are enormous (even with approximations). Now assume $\boldsymbol{A}$ is large but sparse; an SVD decomposition would be far less efficient than the original matrix. CUR decomposition was born for this: it seeks to select $k$ columns to form matrix $\boldsymbol{C}$, $k$ rows to form matrix $\boldsymbol{R}$, and inserts a $k\times k$ matrix $\boldsymbol{U}$ such that:
\begin{equation}\boldsymbol{A} \approx \boldsymbol{C}\boldsymbol{U}\boldsymbol{R}\end{equation}Since $\boldsymbol{C}$ and $\boldsymbol{R}$ are parts of the original matrix, they inherit its sparsity. Regarding CUR decomposition, readers can refer to the "Dimensionality Reduction" section of Stanford's CS246 course. Unlike SVD, CUR decomposition is, in my view, more of a decomposition philosophy than a specific algorithm. It has different implementations, and the Nyström method can be considered one of them, with a form like:
\begin{equation}\begin{pmatrix}\boldsymbol{A} & \boldsymbol{B} \\ \boldsymbol{C} & \boldsymbol{D}\end{pmatrix} \approx \begin{pmatrix}\boldsymbol{A} & \boldsymbol{B} \\ \boldsymbol{C} & \boldsymbol{C}\boldsymbol{A}^{\dagger}\boldsymbol{B}\end{pmatrix} = \begin{pmatrix}\boldsymbol{A} \\ \boldsymbol{C}\end{pmatrix} \boldsymbol{A}^{\dagger} \begin{pmatrix}\boldsymbol{A} & \boldsymbol{B}\end{pmatrix}\end{equation}where $\begin{pmatrix}\boldsymbol{A} \\ \boldsymbol{C}\end{pmatrix}$ and $\begin{pmatrix}\boldsymbol{A} & \boldsymbol{B}\end{pmatrix}$ are selected column and row matrices. For convenience, it is assumed that after Permutation, the selected rows and columns are at the front. Nyströmformer did not directly use the Nyström method (in fact, it cannot be used directly, as described in the paper), but rather borrowed the philosophy of Nyström decomposition.
Regarding the Nyström method, the original paper primarily cites "Improving CUR Matrix Decomposition and the Nyström Approximation via Adaptive Sampling", but I wouldn't recommend that paper for beginners. Instead, I recommend "Matrix Compression using the Nyström Method" and "Using the Nyström Method to Speed Up Kernel Machines".
It should be noted that I am also new to CUR decomposition and the Nyström method; there may be misunderstandings in my interpretation. Please judge for yourself, and I welcome any readers familiar with the theories to exchange ideas and correct me.
This article introduced Nyströmformer, a new piece of work that improves Transformer efficiency. It draws on the ideas of the Nyström method to construct a linear Attention that approximates standard Attention. Performer is another work with similar goals; both have their own pros and cons and are worth studying. I have shared my own understanding of Nyströmformer here, which I believe is slightly more accessible. If there are errors, I kindly ask readers to point them out.
Original Address: https://kexue.fm/archives/8180