From Triangle Inequality to Margin Softmax

By 苏剑林 | September 01, 2021

In "A Sentence Similarity Model Based on GRU and AM-Softmax," we introduced AM-Softmax, a version of Softmax with a margin, which is typically used in scenarios where classification is used for retrieval. At that time, we briefly mentioned through illustrations that the introduction of a margin is due to the "inequivalence between classification and ranking," but we did not provide a relatively quantitative explanation for the source of this inequivalence.

In this article, we revisit this topic to derive and understand the necessity of a margin from the perspective of the triangle inequality for distances.

Triangle Inequality

Usually, when we speak of distance, we generally refer to the intuitive "Euclidean distance." However, in mathematics, distance is also called a "metric," and it has a refined axiomatic definition. It is defined as a binary function $d(x,y)$ on a set that satisfies:

1. Non-negativity: $d(x,y) \geq 0$;
2. Identity: $d(x,y)=0 \Leftrightarrow x = y$;
3. Symmetry: $d(x,y)=d(y,x)$;
4. Triangle Inequality: $d(x,y) \leq d(x,z) + d(z,y)$.

As the name suggests, distance is used to measure the degree of difference between $x$ and $y$. Theoretically, as long as the first two requirements are met, it can be used to measure differences; for example, the commonly used KL divergence in probability satisfies only the first two points. The inclusion of the 3rd and 4th points is essentially to make the distance defined in this way closer to our common Euclidean distance. For instance, symmetry reflects that "distance has no direction," and the triangle inequality reflects that "the shortest distance between two points is a straight line." These analogies allow us to think about more general distances through comparisons with Euclidean distance.

From this definition, deep learning rarely encounters distances that satisfy all four requirements. For example, standard classification directly uses the inner product plus Softmax, where the inner product only satisfies the 3rd point; cosine distance $1-\cos(x,y)$ also only satisfies points 1 and 3, but not 2 and 4 (if we consider all vectors in the same direction as equal, then it could be said to satisfy point 2).

However, we can slightly tweak the definition of certain functions to make them metrics. For example, we know that Euclidean distance satisfies the triangle inequality, so:

must also satisfy the triangle inequality. Therefore, while cosine distance $1-\cos(x,y)$ does not satisfy the triangle inequality, changing it to $\sqrt{1-\cos(x,y)}$ makes it satisfy it.

Classification and Ranking

In scenarios such as face recognition or sentence similarity, we use features for ranking during the prediction phase. We naturally hope that by taking any sample, we can retrieve all samples of the same class, which requires "intra-class variance to be smaller than inter-class variance." However, if we train this as a classification task, we might not achieve this goal because the objective of a classification task is "to be closest to the center of its own class." A specific example can be seen in the figure below:

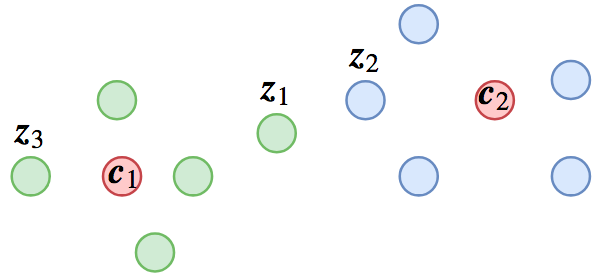
A possible classification result, where red dots represent class centers and other dots represent samples

In this figure, $z_1, z_3$ belong to class $c_1$, and $z_2$ belongs to class $c_2$. From a classification perspective, $d(z_1, c_1) < d(z_1, c_2)$ and $d(z_2, c_2) < d(z_2, c_1)$, so the classification is correct. However, $d(z_1, z_2) < d(z_1, z_3)$, so if we use $z_1$ for retrieval, we find $z_2$ of a different class instead of $z_3$ of the same class.

We can use the triangle inequality to describe this inequality more quantitatively: we want to achieve $d(z_1, z_3) < d(z_1, z_2)$. According to the triangle inequality, $d(z_1,z_3) \leq d(z_1, c_1) + d(z_3, c_1)$, so a sufficient condition is:

Adding $d(z_2, c_2)$ to both sides and using the triangle inequality $d(z_1, z_2) + d(z_2, c_2) \geq d(z_1, c_2)$, we obtain a sufficient condition for the above equation:

Note that the classification task only requires $d(z_1, c_1) < d(z_1, c_2)$ for $z_1$, whereas the equation above has the extra terms $d(z_3, c_1) + d(z_2, c_2)$. These extra terms are the margin terms.

Notice that $d(z_3, c_1)$ and $d(z_2, c_2)$ are the distances from samples $z_3$ and $z_2$ to their respective class centers. We can consider $d(z_3, c_1) + d(z_2, c_2)$ as the "average class diameter," which should be close to a constant $m$ that we can tune as a hyperparameter. If adaptive adjustment is desired, one could consider training with $m=0$ for a period, then estimating the "average class diameter" to use as $m$ for further training, re-estimating $m$, and so on.

AM-Softmax

Through the derivation above, we know that to ensure the features of a classification model can be used for ranking, each sample must not only be closest to its class center, but also remain closest to the class center even after adding $m$ to the distance. That is, if $z_1$ belongs to class $c_1$, then we require:

Following the logic in "Generalizing 'Softmax + Cross Entropy' to Multi-label Classification," whenever we want $s_i < s_j$, we can construct a loss by adding $e^{s_i - s_j}$ inside a $\log$. Thus, we can construct the following loss:

This is the cross-entropy with an additive margin, where $s$ is the scaling ratio, equivalent to the temperature parameter in Softmax.

However, do not forget that the derivation above assumes that $d$ satisfies the triangle inequality, while the scoring functions we usually use might not. When training retrieval models, we typically use cosine distance for scoring. As mentioned earlier, cosine distance can satisfy the triangle inequality by taking the square root. Therefore, the requirements become (using $i=2$ as an example):

Multiplying both sides by $\sqrt{1-\cos(z_1, c_2)} + \sqrt{1-\cos(z_1, c_1)}$, we get:

Clearly, the right-hand side is bounded. Therefore, by appropriately adjusting $m$, we can make:

a sufficient condition. In this case, the corresponding margin cross-entropy is:

This is AM-Softmax.

Review and Summary

This article derives the necessity of a margin when using a classification model for ranking tasks from the perspective of the triangle inequality. Assuming the scoring function used satisfies the triangle inequality, relevant results can be derived quite naturally.