Bidirectional Decoding in seq2seq

By 苏剑林 | August 09, 2019

In the article "Playing with Keras: seq2seq for Automatic Title Generation," we basically explored seq2seq and provided a reference implementation in Keras.

This article takes that seq2seq model one step further by introducing a bidirectional decoding mechanism. This can improve the quality of generated text to a certain extent (especially when generating longer texts). The bidirectional decoding mechanism introduced here is based on "Synchronous Bidirectional Neural Machine Translation," and the author has implemented it using Keras.

Background Introduction

Readers who have studied seq2seq know that common seq2seq decoding processes generate text word-by-word (or character-by-character) from left to right. This involves generating the first word based on the encoder's output, then generating the second word based on the encoder's output and the generated first word, then the third word based on the encoder's output and the first two words, and so on. In general, this models the following probability decomposition:

Of course, generation could also proceed from right to left, meaning the last word is generated first, then the second-to-last, and so on. The problem is that regardless of which direction is used, there is an issue of directional bias. For example, if generating from left to right, the accuracy of the first few words will definitely be higher than the last few words, and vice versa. The paper "Synchronous Bidirectional Neural Machine Translation" provides the following statistical results on a machine translation task:

L2R and R2L refer to Left-to-Right and Right-to-Left decoding, respectively. From the table, we can see that if decoding is L2R, the accuracy of the first four tokens is about 40%, but the accuracy of the last four tokens is only 35%; it is similar in reverse. This reflects the asymmetry of decoding.

To eliminate this asymmetry, "Synchronous Bidirectional Neural Machine Translation" proposes a bidirectional decoding mechanism. it maintains two directional decoders and uses Attention to further align the generation.

Bidirectional Decoding

Although this article is based on "Synchronous Bidirectional Neural Machine Translation," I did not read the original text in its entirety. I roughly understood the principle based on my intuition and implemented the model myself, so I cannot guarantee it is exactly identical to the original paper. Furthermore, this paper is not the first to work on bidirectional decoding, but it is the first one I encountered, so I only implemented this specific approach and did not compare it with other related papers.

Basic Idea

Since it is called bidirectional "decoding," the changes are only in the decoder and do not involve the encoder. Therefore, the following description focuses on the decoder part. Also, note that bidirectional decoding is just a strategy, and the following is merely one reference implementation, not a standard or unique one. This is just like saying seq2seq is a general term for sequence-to-sequence generation models; the specific design of the encoder and decoder has many adjustable components.

First, here is a simple animated illustration to demonstrate the design and interaction process of the bidirectional decoding mechanism:

Illustration of the Seq2Seq Bidirectional Decoding Mechanism

As shown in the figure, bidirectional decoding essentially consists of two co-existing decoding modules for different directions. For descriptive convenience, we call the upper one the L2R module and the lower one the R2L module. At the start, both are input with a start token (S in the figure). Then, the L2R module is responsible for predicting the first word, while the R2L module is responsible for predicting the last word. Next, the first word (and historical information) is passed to the L2R module to predict the second word. To predict the second word, in addition to using the L2R module's own encoding, the existing encoding result from the R2L module is also used. Conversely, the last word (and history) is passed to the R2L module, and combined with the existing L2R encoding information, used to predict the second-to-last word; and so on, until the end token (E in the figure) appears.

Mathematical Description

In other words, when each module predicts each word, in addition to using information internal to the module, it also uses the sequence of information already encoded by the other module, and this "usage" is realized through Attention. Formally, assume that in the current step, the L2R module needs to predict the $n$-th word, and the R2L module needs to predict the $n$-th word from the end. Suppose that after several layers of encoding, the obtained L2R vector sequence (corresponding to the second row at the top left in the figure) is:

And the R2L vector sequence (corresponding to the second-to-last row at the bottom left in the figure) is:

In unidirectional decoding, we would use $h_n^{(l2r)}$ as the feature to predict the $n$-th word, or use $h_n^{(r2l)}$ as the feature to predict the $n$-th word from the end.

Under the bidirectional decoding mechanism, we use $h_n^{(l2r)}$ as a query, and then use $H^{(r2l)}$ as keys and values to perform an Attention. The output of the Attention is used as the feature to predict the $n$-th word. Thus, when predicting the $n$-th word, it can "perceive" the subsequent words in advance. Similarly, we use $h_n^{(r2l)}$ as a query, and use $H^{(l2r)}$ as keys and values to perform an Attention. The Attention output is used as the feature to predict the $n$-th word from the end, allowing it to "perceive" the preceding words in advance. In the diagram above, the interaction between the top two layers and the bottom two layers refers to this Attention. In the code below, standard multiplicative Attention is used (refer to "A Light Reading of 'Attention is All You Need' (Introduction + Code)").

Model Implementation

The above describes the basic principle and approach of bidirectional decoding. It can be felt that in this way, the seq2seq decoder also becomes symmetric, which is a very beautiful feature. Of course, to fully implement this model, one must consider: 1. How to train? 2. How to predict?

Training Scheme

Just like standard seq2seq, the basic training scheme uses the "Teacher-Forcing" method. The L2R direction, when predicting the $n$-th word, assumes the previous $n-1$ words are known accurately; the R2L direction, when predicting the $n$-th word from the end, assumes the words from the end $n-1, n-2, \dots, 1$ are known accurately. The final loss is the average of the word-by-word cross-entropy in both directions.

However, such a training scheme is a necessary compromise, as we will later analyze its drawback regarding information leakage.

Bidirectional Beam Search

Now, let's discuss the prediction process.

In a conventional unidirectional seq2seq, we use the Beam Search algorithm to provide a sequence with the highest possible probability. Beam search refers to decoding word-by-word, keeping only the top-k "temporary paths" with the highest probabilities at each step until an end token appears.

In bidirectional decoding, the situation becomes more complex. We still use the beam search idea, but simultaneously cache top-k results for both directions. That is, L2R and R2L each store top-k temporary paths. Furthermore, since L2R decoding refers to R2L's existing decoding results, when we want to predict the next word, in addition to enumerating the top-k most probable words and the top-k L2R temporary paths, we also have to enumerate the top-k R2L temporary paths. This results in calculating $topk^3$ combinations. After calculation, a simple approach is adopted: the score of each "word - L2R temporary path" is averaged over the "R2L temporary path" dimension, reducing the scores back to $topk^2$, which serves as the score for each "word - L2R temporary path." From these $topk^2$ combinations, the top-k highest scoring ones are selected. R2L decoding undergoes an identical reverse process. Finally, if both L2R and R2L directions have decoded complete sentences, the sentence with the highest probability (score) is chosen.

This entire process is called "Bidirectional Beam Search." If readers are familiar with unidirectional beam search or have written it themselves, the above process is actually not hard to understand (it is even easier to understand by looking at the code); it can be considered a natural extension of unidirectional beam search. Of course, if one is unfamiliar with beam search itself, the description above might seem confusing. Therefore, readers wanting to understand the principle should start from standard unidirectional beam search, understand it thoroughly, then read the description of the decoding process above, and finally look at the reference code provided below.

Code Reference

Below is the reference implementation of bidirectional decoding. The overall structure is consistent with the previous "Playing with Keras: seq2seq for Automatic Title Generation," except the decoding end has been changed from unidirectional to bidirectional:

https://github.com/bojone/seq2seq/blob/master/seq2seq_bidecoder.py

Note: The test environment is similar to before, roughly Python 2.7 + Keras 2.2.4 + Tensorflow 1.8. For friends using Python 3.x or other environments, if you can modify it yourself, please make the corresponding changes; if you cannot, please do not ask me. I really do not have time or obligation to help run it in every environment. Can we only discuss content related to seq2seq technology in this article?

In this implementation, I think it is necessary to explain the start and end tokens. In the previous unidirectional decoding example, I used 2 as the start token and 3 as the end token. In bidirectional decoding, a natural question is whether the L2R and R2L directions should use two separate sets of start and end tokens.

Actually, there isn't a standard answer. I believe whether sharing one set or maintaining two sets of markers, the results might be similar. As for the reference code above, I used a slightly unconventional but intuitive approach: still only one set, but in the L2R direction, 2 is used as the start token and 3 as the end token; while in the R2L direction, 3 is used as the start token and 2 as the end token.

Analysis and Refelction

Finally, let's think deeper about this bidirectional decoding scheme. Although symmetrizing the decoding process is a beautiful feature, it doesn't mean it is without issues. Thinking about it more deeply helps us understand and use it better.

1. Reason for Improvement in Generation

An interesting question is: while bidirectional decoding seems to improve generation quality at the beginning and end of a sentence, does it simultaneously reduce the quality in the middle?

Theoretically, this is possible, but it is not very serious in actual tests. On one hand, the information encoding and decoding capabilities of the seq2seq architecture are strong, so information is not easily lost. On the other hand, when we evaluate the quality of a sentence ourselves, we often focus on the start and end. If the start and end are reasonable and the middle part is not too terrible, we tend to consider it a reasonable sentence. Conversely, if the start or end is unreasonable, we find the sentence poor. Thus, by improving the quality of the sentence's start and end, the overall generation quality is improved.

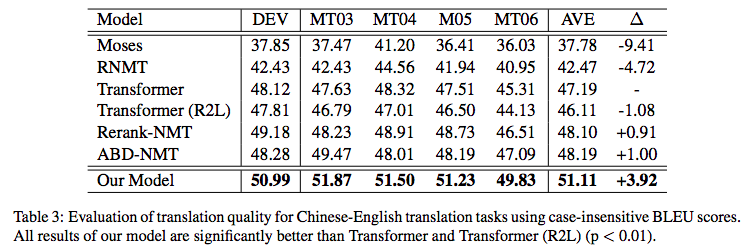
Improvement brought by bidirectional decoding relative to other unidirectional models in the original paper

2. Lack of Correspondence to a Probability Model

For unidirectional decoding, we have a clear probabilistic interpretation, which is estimating the conditional probability $p(Y|X)$ (Equation $\eqref{eq:p}$). However, in bidirectional decoding, we find that we don't know how to correspond it to a probability model. In other words, we feel we are calculating probabilities and seeing results, but we don't know what we are truly calculating because the dependencies of the conditional probability have been completely scrambled.

Of course, if there is practical effectiveness, theoretical beauty matters less. The point I'm making is just a pursuit of theoretical aesthetics; whether it matters is a matter of opinion.

3. Early Information Leakage

Information leakage refers to the phenomenon where the labels intended as the prediction target are used as inputs, leading to a deceptively low loss (or deceptively high accuracy) during the training phase.

Because in bidirectional decoding, the L2R end needs to read the vector sequence already existing at the R2L end, and in the training phase, to predict the $n$-th word at the R2L end, the previous $n-1$ words are passed in. Consequently, the further decoding progresses, the more serious the information leakage becomes. As shown below:

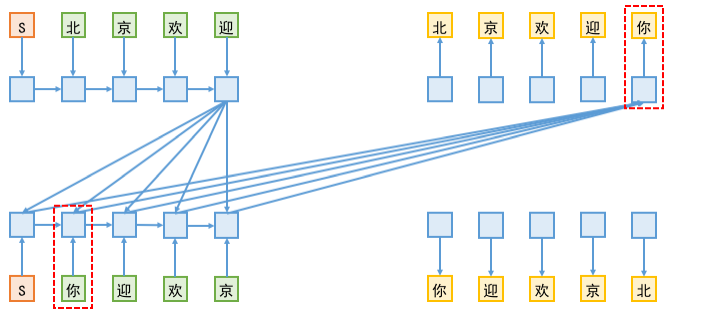
Information leakage illustration. In the training phase, when the L2R end predicts "你", it actually uses the label "你" passed to the R2L end; conversely, when the R2L end predicts "北", the same problem exists, as it uses the L2R "北" label.

One manifestation of information leakage is that late in training, the sum of cross-entropies for the L2R and R2L directions in bidirectional decoding is smaller than a single cross-entropy when training a unidirectional model alone. This is not because bidirectional decoding brings a massive improvement in fitting, but is purely a manifestation of information leakage.

Since information is leaked during training, why is such a model still useful? I think the reason is provided in the table at the beginning of the article. Using the same example, when the L2R end predicts the last word "你", it uses all known information from the R2L end. R2L decodes word-by-word from right to left. According to the statistics in the table at the beginning, it's not hard to imagine that the prediction accuracy of the first word (the last word of the sentence) for the R2L end should be the highest. Thus, assuming R2L's last word can indeed be predicted successfully with high accuracy, information leakage becomes non-leakage—because leakage occurs because we manually passed in labels, but if the predicted result itself matches the label, the leakage is no longer a "leak."

Of course, the original paper provides a strategy to mitigate this leakage problem. The general approach is to first train a version of the model as described above, then for each training sample, use the model to generate the corresponding prediction results (pseudo-labels). Then, train the model again, but this time pass in pseudo-labels to predict the correct labels, maintaining consistency between training and prediction as much as possible.

Article Summary

This article introduced and implemented a bidirectional decoding mechanism for seq2seq, which symmetrizes the entire decoding process, thereby leading to higher generation quality to some extent. Personally, I believe this attempt at improvement has certain value, especially for readers who pursue formal beauty. Therefore, I have introduced it here.

Additionally, the article analyzed potential problems with this bidirectional decoding and provided the author's own views. We look forward to communicating more with our readers!