By 苏剑林 | April 07, 2022
I don't know if you've noticed a detail: the current mainstream NLP pre-training mode is carried out on a fixed length (such as 512), and then the pre-trained model is directly applied to tasks of different lengths. It seems that no one has ever doubted this mode, as if it's "taken for granted" that the model can automatically generalize to different lengths.
Of course, I hadn't questioned this either until a few days ago when I conducted Base-version GAU experiments. I found that the length generalization ability of GAU was not as good as imagined. After further analysis, I finally understood that this length generalization ability is not "naturally occurring"...
Model Review
In "FLASH: Perhaps the Most Interesting Efficient Transformer Design Recently," we introduced the "Gated Attention Unit (GAU)," which is a new design that integrates GLU and Attention.
Aside from its performance, GAU brought us two main design shocks: first, it showed that single-head attention is not necessarily inferior to multi-head attention, which established its status as being "fast" and "efficient"; second, it showed that attention does not necessarily require Softmax normalization and can be replaced by a simple $\text{relu}^2$ divided by the sequence length:
\begin{equation}\boldsymbol{A}=\frac{1}{n}\text{relu}^2\left(\frac{\mathcal{Q}(\boldsymbol{Z})\mathcal{K}(\boldsymbol{Z})^{\top}}{\sqrt{s}}\right)=\frac{1}{ns}\text{relu}^2\left(\mathcal{Q}(\boldsymbol{Z})\mathcal{K}(\boldsymbol{Z})^{\top}\right)\end{equation}
This form leads to an interesting question: if we try to organize samples into the same length (say 512) during the pre-training stage, then $n$ is almost always 512 throughout pre-training. In other words, $n$ acts as a constant. When we use it for fine-tuning on other lengths (such as 64 or 128), should this $n$ automatically change to the sample length, or remain at 512?
Intuitively, making it equal to the sample length should be more adaptive, but the answer is counter-intuitive: fine-tuning with $n$ fixed at 512 is significantly better than setting $n$ to the sample length! This is thought-provoking...
Locating the Problem
If we look only at GAU's pre-training performance, it is superior to standard Attention. Therefore, GAU's inherent fitting ability should be fine; it's just that $\frac{1}{n}\text{relu}^2(\cdot)$ has poor transferability regarding sample length. To confirm this, I also tried mixed-length sample pre-training for GAU and found that the results improved significantly.
So, what could be the issue with GAU? It's not hard to guess. The overall calculation of GAU can be simplified as $\boldsymbol{O}=(\boldsymbol{U}\odot\boldsymbol{A}\boldsymbol{V})\boldsymbol{W}_o$, where $\boldsymbol{U}, \boldsymbol{V}, \boldsymbol{W}_o$ are all token-wise. This means they are not affected by length changes at all, so the problem must lie in $\boldsymbol{A}$.
When we used standard Attention in the past, we didn't encounter similar problems, so much so that we unconsciously felt this was a "natural" property. Therefore, we need to find the problem in the differences between GAU's Attention and standard Attention. As mentioned before, there are two differences: one is that multi-head Attention becomes single-head Attention, but this would at most cause some fluctuation in performance, while our results showed a sharp decline. Thus, the problem can only lie in the other point: the normalization method, specifically the change from Softmax to $\frac{1}{n}\text{relu}^2(\cdot)$.
Verifying this guess is simple. I replaced the normalization method in GAU's Attention back to Softmax, re-trained a GAU model, and then fine-tuned it on tasks of different lengths. I found that its performance was significantly better than when using $\frac{1}{n}\text{relu}^2(\cdot)$. Thus, we conclude: Attention and Softmax are indeed a better match.
Reason Analysis
Why does the more intuitive, length-adaptive $n$ perform worse than a fixed $n$? Since we know Softmax doesn't have this problem, let's look at Softmax for inspiration. The Softmax operation is:
\begin{equation}a_{i,j} = \frac{1}{Z_i}\exp\left(\frac{\boldsymbol{q}_i\cdot\boldsymbol{k}_j}{\sqrt{d}}\right),\quad Z_i = \sum_{j=1}^n \exp\left(\frac{\boldsymbol{q}_i\cdot\boldsymbol{k}_j}{\sqrt{d}}\right)\end{equation}
An immediate question is: what is the relationship between $Z_i$ and $n$? If $Z_i=\mathcal{O}(n)$ were truly the case, then replacing $Z_i$ with $n$ should theoretically yield similar results, or at least not terrible ones.
However, we know that the core of attention is to "attend"—it should have the ability to "focus" on a few tokens it deems important. Meanwhile, previous experimental results on efficient Transformers showed that replacing standard Attention with Local Attention does not cause a significant drop in results. Thus, we can expect that the Attention at position $i$ focuses mainly on a few tokens near $i$, and drops to basically zero beyond a certain distance. In fact, many post-hoc visualization results show that the trained Attention matrices are very sparse.
Synthesizing these results, we can conclude that there exists some constant $k$ such that when $|j-i| \geq k$, $\exp\left(\frac{\boldsymbol{q}_i\cdot\boldsymbol{k}_j}{\sqrt{d}}\right)$ is very close to 0. Consequently, $Z_i$ should be closer to $\mathcal{O}(k)$ rather than $\mathcal{O}(n)$, which means $Z_i$ is likely independent of $n$, or at least its order of magnitude relative to $n$ is less than $\mathcal{O}(n)$! Therefore, if we want to replace $Z_i$ with something else, it should be a function of a lower order than $n$ to the power of one, or even a constant.
Now looking back at GAU, when its activation function is changed to $\text{relu}^2(\cdot)$, the Attention situation is similar, or even sparser. This is because the $\text{relu}$ operation has a direct zeroing effect, unlike $\exp(\cdot)$ which is always positive. Additionally, GAU comes "standard" with Rotary Positional Embedding (RoPE). In "Transformer Upgrade: 2. Rotary Positional Embedding", we derived that RoPE itself has a certain long-range decay capability. Combining these factors, GAU's normalization factor should also be of an order lower than $\mathcal{O}(n)$, or even constant.
Entropy Invariance
From this, we can summarize three solutions for GAU: first, use the same fixed $n$ for both pre-training and fine-tuning; second, continue using the dynamic sample length $n$, but mix samples of different lengths during pre-training instead of using a single length; third, add a normalization factor like Softmax and let the model learn it:
\begin{equation}a_{i,j} = \frac{1}{Z_i}\text{relu}^2\left(\frac{\boldsymbol{q}_i\cdot\boldsymbol{k}_j}{\sqrt{d}}\right),\quad Z_i = \sum_{j=1}^n \text{relu}^2\left(\frac{\boldsymbol{q}_i\cdot\boldsymbol{k}_j}{\sqrt{d}}\right)\end{equation}
Since these solutions exist, why do we say "Attention and Softmax are a better match"? What makes GAU's $\text{relu}^2(\cdot)$ a poor match? First, if we look at the ablation experiments in the original GAU paper, they show that replacing $\text{relu}^2(\cdot)$ with Softmax yields basically identical performance:
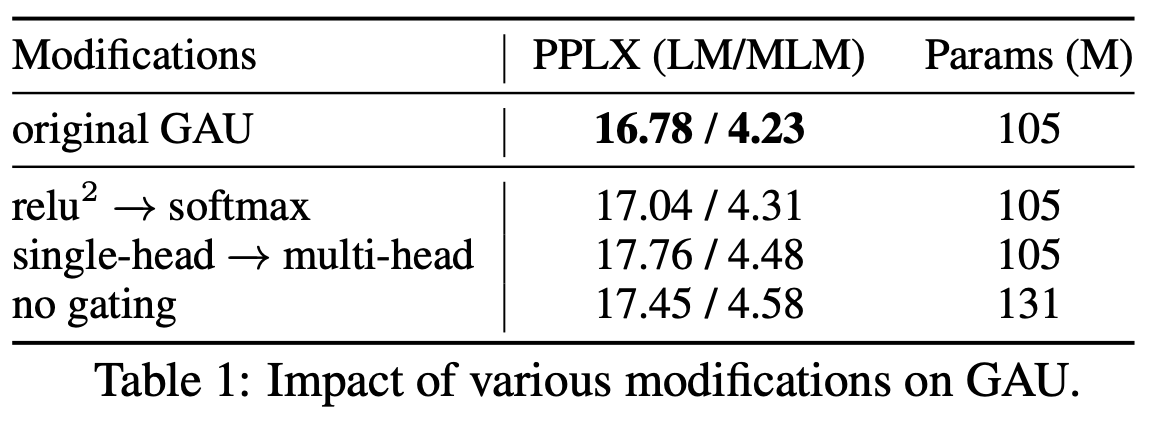
Replacing GAU's squared_relu with softmax yields similar performance
With this basic guarantee, we can see why Softmax is better than $\text{relu}^2(\cdot)$. Among the three solutions mentioned, Solution 1 feels insufficiently adaptive, and Solution 2 requires training with multiple lengths, which feels less elegant. As for Solution 3, the form actually becomes "bulky" compared to Softmax after adding the normalization factor. Thus, overall, Softmax appears more elegant and effective.
Furthermore, generalization can be divided into "interpolation" and "extrapolation." Here, interpolation (extrapolation) refers to test lengths being shorter (longer) than training lengths. When we said the normalization factor is of a constant magnitude, we were mostly talking about interpolation. For extrapolation, if the length becomes long enough, $\boldsymbol{q}_i, \boldsymbol{k}_j$ are all "crowded" together, making it difficult to maintain the property of approaching 0 beyond a certain range. If we use Softmax, we can derive an "entropy-invariant" version to enhance the model's extrapolation capability:
\begin{equation}Attention(Q,K,V) = \text{softmax}\left(\frac{\log_{512} n}{\sqrt{d}}QK^{\top}\right)V\end{equation}
In "Looking at Attention Scale Operations from Entropy Invariance," we performed simple comparative experiments showing that this version indeed improves performance beyond the training length.
So, can $\text{relu}^2(\cdot)$ derive an "entropy-invariant" version? The answer is no, because that would require adjusting the distribution's entropy via a temperature parameter, which requires the activation function to not possess positive homogeneity. For example, for a power function, $(\lambda \boldsymbol{q}_i \cdot \boldsymbol{k}_j)^n = \lambda^n (\boldsymbol{q}_i \cdot \boldsymbol{k}_j)^n$; after normalization, $\lambda^n$ cancels out and has no effect. The activation function should preferably be one order higher than a power function to achieve this regulation. The most common functions higher-order than power functions are exponential functions, and exponential normalization is exactly Softmax.
Summary
This article analyzed the reasons for GAU's poor fine-tuning performance and discovered that the normalization factor for Attention should be close to a constant magnitude. Therefore, using $n$ or $n^2$ as a normalization factor in GAU leads to poor performance. Generally, I believe Attention is still a better match with Softmax; it provides a good baseline and can further enhance extrapolation capabilities through "entropy invariance" extensions.